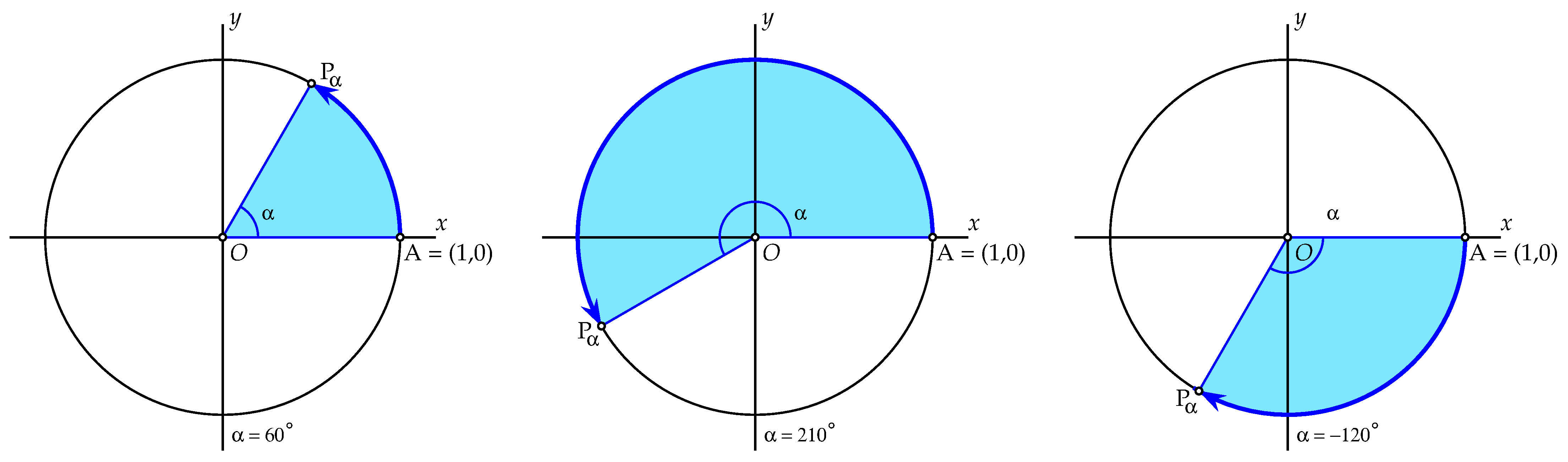
Let us have a look at a point \(P_{\alpha}\) on the unit circle obtained after rotating the point \(A=(1,0)\) about the origin over a certain angle of rotation \(\alpha\). In case of a positive angle of rotation \(\alpha\) we rotate anticlockwise; a negative angle of rotation \(\alpha\) means by convention a rotation in the clockwise direction. A full anticlockwise turn measures \(360^\circ\). The below figure shows some positive and negative angles of rotation.

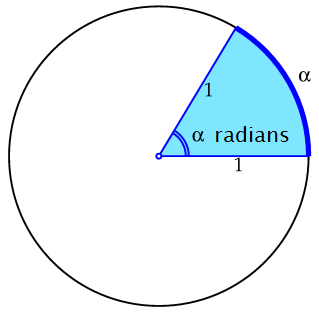
A rotation angle is usually specified in degrees. But with the unit circle, we can also introduce the angular measure radian, abbreviated as the unit \(\mathrm{rad}\). For points \(A\) and \(P_\alpha\) on the unit circle, the central angle is \(AOP_{\alpha}\) in radians equal to the arc length of the corresponding circular arc \(AP_{\alpha}\). Angle \(\alpha\) in degrees and arc length are in essence interchangeable positive quantities.

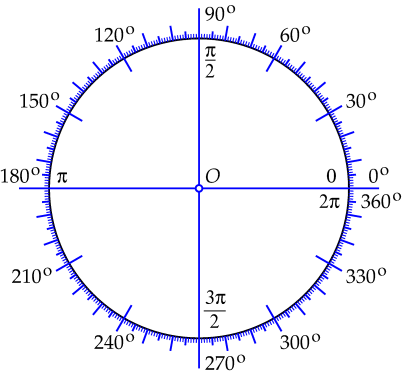
The entire unit circle has circular arc length \(2\pi\) and a full anticlockwise turn measures \(360^\circ\). It follows directly that \(2\pi\;\mathrm{rad}=360^{\circ}\), so \(\pi\;\mathrm{rad}=180^{\circ}\). To convert degrees to radians and vice versa, you can use a ratio table. \[\begin{array}{r|c|c|c|c|c} \mathrm{degrees} & 360^{\circ} & 180^{\circ} & 90^{\circ} & \frac{180^{\circ}}{\pi} & 1^{\circ}\\ \hline \mathrm{radians} & 2\pi & \pi & \tfrac{1}{2}\!\pi & 1 & \frac{\pi}{180} \end{array}\] In the figure below you see the unit circle with indications for both scales.

For rotations, the angle of rotation can also be greater than \(360^{\circ}\) ( \(2\pi\) radians). For the final position of rotated points it does not matter whether you are add or subtract integer multiples of \(360^{\circ}\) (or \(2\pi\) radians).

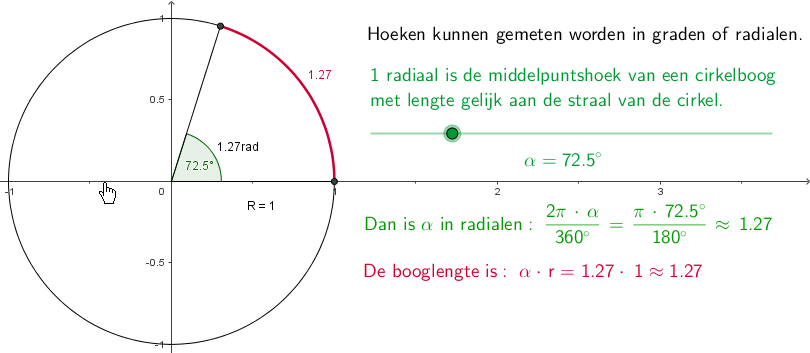
Interactive example Below is an interacteve version about the relationship between an angle of rotation and the arc length of a unit circle; move the slider to explore various configurations.