Eenheidscirkel Onder de eenheidscirkel in het vlak verstaan we de cirkel met de oorsprong \(O=(0,0)\) als middelpunt en straal 1.

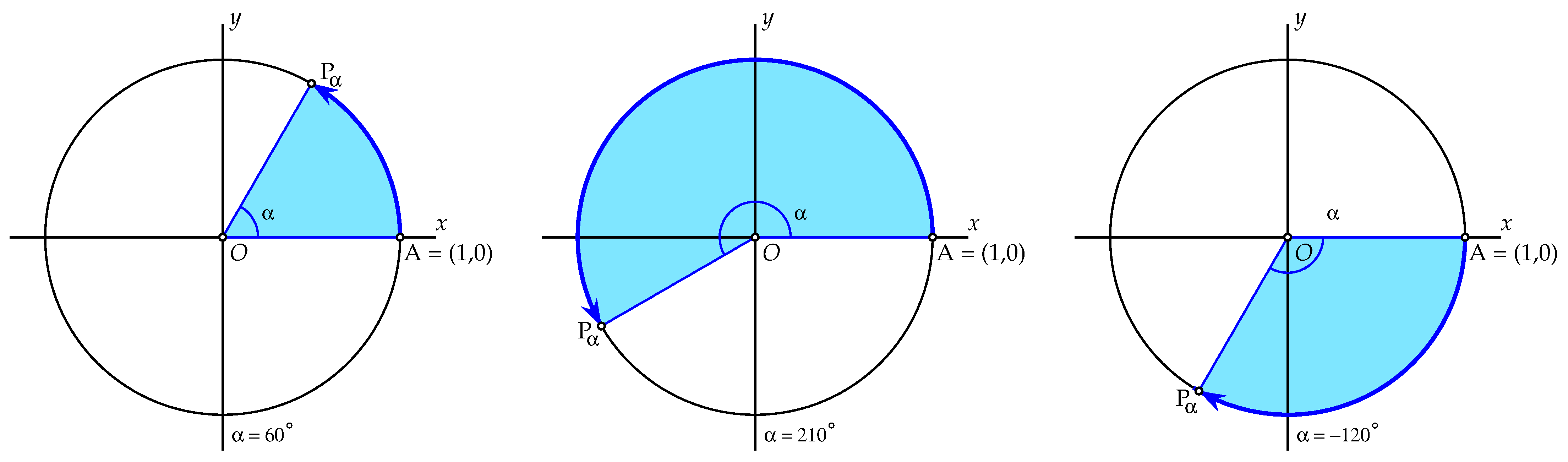
Draaiingshoek Laten we nu een punt \(P_{\alpha}\) op de eenheidscirkel bekijken dat verkregen is door draaiing van het punt \(A=(1,0)\) over een zekere draaiingshoek \(\alpha\). Bij een positieve draaiingshoek \(\alpha\) draaien we tegen de wijzers van de klok in; een negatieve draaiingshoek \(\alpha\) betekent een draaiing met de wijzers van de klok mee. Een volledige rondgang tegen de wijzers van de klok in is een draaiingshoek van \(360^\circ\). Onderstaande figuur toont enkele positieve en negatieve draaiingshoeken.

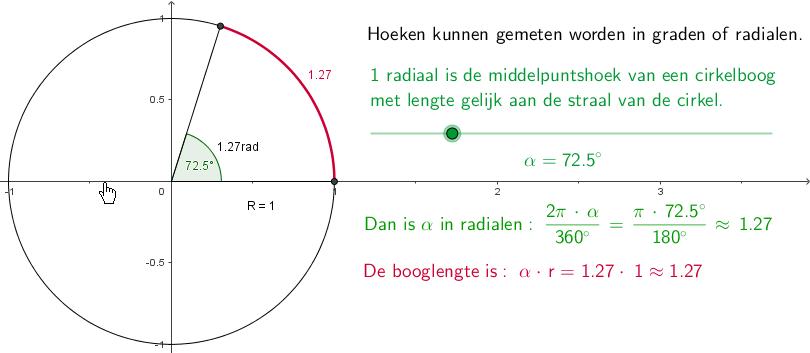
Een draaiingshoek specificeren we meestal in graden. Maar met de eenheidscirkel kunnen we ook de hoekmaat radiaal introduceren, afgekort als de eenheid \(\mathrm{rad}\). Voor de punten \(A\) en \(P_\alpha\) op de eenheidscirkel is de middelpuntshoek \(AOP_{\alpha}\) in radialen gelijk aan de booglengte van de bijbehorende cirkelboog \(AP_{\alpha}\). Hoek \(\alpha\) in graden en booglengte zijn in wezen uitwisselbaar voor positieve grootheden.

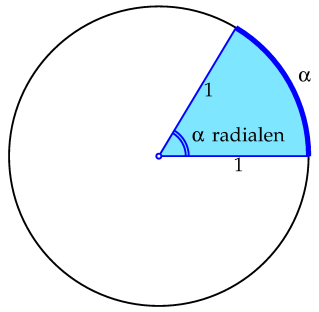
Radiaal Een hoek van 1 radiaal is de middelpuntshoek in de eenheidscirkel die hoort bij een cirkelboog met lengte 1.

De hele eenheidscirkel heeft booglengte \(2\pi\) en een volledige rondgang is een draaiingshoek van \(360^\circ\). Hieruit volgt direct \(2\pi\;\mathrm{rad}=360^{\circ}\), dus \(\pi\;\mathrm{rad}=180^{\circ}\). Voor het omzetten van graden in radialen en omgekeerd kun je gebruikmaken van een verhoudingstabel zoals hieronder staat.

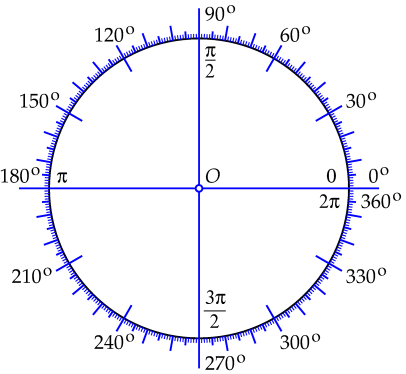
\[\begin{array}{r|c|c|c|c|c} \mathrm{graden} & 360^{\circ} & 180^{\circ} & 90^{\circ} & \frac{180^{\circ}}{\pi} & 1^{\circ}\\ \hline \mathrm{radialen} & 2\pi & \pi & \tfrac{1}{2}\!\pi & 1 & \frac{\pi}{180} \end{array}\] In onderstaande figuur zie je de eenheidscirkel in het vlak waarop de beide verdelingen voor hoekmaat zijn aangegeven.

Bij draaiingen kan een draaiingshoek kan natuurlijk ook groter dan \(360^{\circ}\) (\(2\pi\) radialen) zijn. Voor het resultaat maakt het niets uit of je er gehele veelvouden van \(360^{\circ}\) (of \(2\pi\) radialen) bij optelt of van aftrekt.