Trigonometry: Trigonometric functions
 Basic properties of trigonometric functions
Basic properties of trigonometric functions
Properties of goniometric functions Some properties of the trigonometric functions follow almost directly from the definitions.
Basic rule
Example
\[\begin{aligned}\cos^2(\tfrac{1}{6}\pi)+\sin^2(\tfrac{1}{6}\pi) &= \left(\tfrac{1}{2}\sqrt{3}\right)^2+\left(\tfrac{1}{2}\right)^2\\[0.25cm] &= \tfrac{3}{4}+\tfrac{1}{4}= 1\end{aligned}\]
Periodicity
Examples
\[\begin{aligned}\sin(\tfrac{7}{3}\pi) &= \sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(-\tfrac{2}{3}\pi) &= \cos(\tfrac{4}{3}\pi)\\[0.25cm] \tan(-\tfrac{1}{3}\pi) &= \tan(\tfrac{2}{3}\pi)\end{aligned}\]
Mirror symmetry
From the definitions follow directly the below symmetry properties:
- Reflection in the horizontal axis leads to: \[\begin{aligned} \sin(-\alpha)&=-\sin(\alpha)\\[0.25cm] \cos(-\alpha)&=\cos(\alpha)\\[0.25cm] \tan(-\alpha)&=-\tan(\alpha)\end{aligned}\]
- Reflection in the vertical axis leads to: \[\begin{aligned}\sin(\pi-\alpha)&=\sin(\alpha)\\[0.25cm] \cos(\pi-\alpha)&=-\cos(\alpha)\\[0.25cm] \tan(\pi-\alpha)&=-\tan(\alpha)\end{aligned}\]
- Reflection in the slanted line \(y=x\) leads to: \[\begin{aligned}\sin(\tfrac{1}{2}\pi-\alpha)&=\cos(\alpha)\\[0.25cm] \cos(\tfrac{1}{2}\pi-\alpha)&=\sin(\alpha)\\[0.25cm] \tan(\tfrac{1}{2}\pi-\alpha)&=\frac{1}{\tan(\alpha)}\end{aligned}\]
Examples
\[\begin{aligned}\sin(-\tfrac{1}{3}\pi) &= -\sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(-\tfrac{1}{3}\pi) &= \cos(\tfrac{1}{3}\pi)\\[0.25cm] \tan(-\tfrac{1}{3}\pi) &= -\tan(\tfrac{1}{3}\pi)\end{aligned}\]
\(\phantom{abc}\)
\[\begin{aligned}\sin(\tfrac{2}{3}\pi) &= \sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(\tfrac{2}{3}\pi) &= -\cos(\tfrac{1}{3}\pi)\\[0.25cm] \tan(\tfrac{2}{3}\pi) &= -\tan(\tfrac{1}{3}\pi)\end{aligned}\]
\(\phantom{abc}\)
\[\begin{aligned}\sin(\tfrac{1}{3}\pi) &= \cos(\tfrac{1}{6}\pi)\\[0.25cm] \cos(\tfrac{1}{3}\pi) &= \sin(\tfrac{1}{6}\pi)\\[0.25cm] \tan(\tfrac{1}{3}\pi) &= \frac{1}{\tan(\tfrac{1}{6}\pi)}\end{aligned}\]
Domain and range From the definition also follows immediately that the range of the sine and cosine function is equal to the segment [-1,1], and that the domain consists of all real numbers. The range of the tangent function is made up of all the real numbers, and the domain consists of all real numbers other than the numbers that are equal to \(\tfrac{1}{2}\pi\) modulo \(\pi\).
Special function values Some domain values have special values for sine, cosine and tangent, which you should know by heart, or can derive in no time and effort from the Pythagorean theorem: \[
\begin{array}{r|ccccc}
\alpha & 0 & \tfrac{1}{6}\pi & \tfrac{1}{4}\pi & \tfrac{1}{3}\pi & \tfrac{1}{2}\pi
\\ \hline &&&&& \\
\sin \alpha & 0 & \tfrac{1}{2} & \tfrac{1}{2}\sqrt{2} & \tfrac{1}{2}\sqrt{3} & 1 \\ &&&&& \\
\cos \alpha & 1 & \tfrac{1}{2}\sqrt{3} & \tfrac{1}{2}\sqrt{2} & \tfrac{1}{2} & 0 \\ &&&&& \\
\tan \alpha & 0 & \tfrac{1}{3}\sqrt{3} & 1 & \sqrt{3} & - \\
\end{array}
\]
Suppose that you want to compute the function values \(\sin(\tfrac{1}{6}\pi)\), \(\cos(\tfrac{1}{6}\pi)\) and \(\tan(\tfrac{1}{6}\pi)\). This corresponds with a point \(B\) on the unit circle which together with the origin (designated by the letter \(A\) ) and the vertical projection of \(B\) on the horizontal axis (designated by the letter \(C\) ) forms the vertices of a right-angled triangle as in the figure below
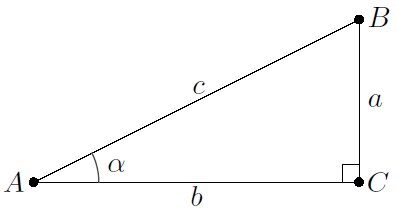
with \(c=1\), \(\alpha=\tfrac{1}{6}\pi\) and \(a=\dfrac{1}{2}\) (the latter formula follows from the fact that mirroring the triangle in the horizontal line leads to an equilateral triangle with sides of length 1) The Pythagorean theorem then leads to \(b^2=c^2-a^2=\dfrac{3}{4}\) and thus \(b=\tfrac{1}{2}\!\sqrt{3}\). Then, by definition, we have \[\cos(\tfrac{1}{6}\!\pi) = \tfrac{1}{2}\!\sqrt{3}, \qquad\sin(\tfrac{1}{6}\!\pi) =\tfrac{1}{2} \qquad\text{ and }\qquad\tan(\tfrac{1}{6}\!\pi) = \dfrac{1}{\sqrt{3}}= \tfrac{1}{3}\!\sqrt{3}\tiny.\]
Exact-values-circls With the symmetry properties and the special values, you can also calculate other special function values. They are shown in the exact-values-circle.
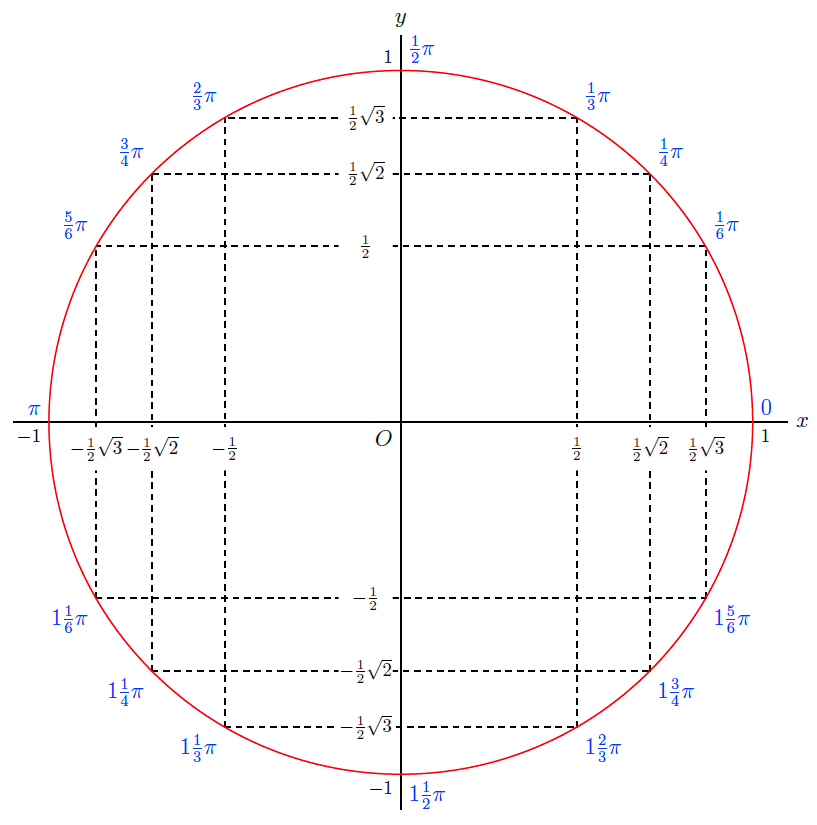
Given \(\sin(\tfrac{1}{3}\!\pi)=\tfrac{1}{2}\!\sqrt{3}\), what is \(\sin(\tfrac{2}{3}\!\pi)\)?
If \(t=\tfrac{23}{6}\pi\) and we follow the above steps, we get: \[\begin{array}{rclcl}\cos(\tfrac{23}{6}\pi) &=& \cos(\tfrac{23}{6}\pi-4\pi)\;=\;\cos(-\tfrac{1}{6}\pi)&\phantom{xx}& \blue{\text{period }2\pi}\\ &=& \cos(\tfrac{1}{6}\pi)&\phantom{xx}& \blue{\text{reflection in }x\text{-as}}\\ &=&\tfrac{1}{2}\sqrt{3} &\phantom{xx}& \blue{\text{special value}}\end{array}\]
Strategy for the calculation of trigonometric function values For domain values that are not within \([0,2\pi]\), use first the periodic behaviour of the trigonometric functions in order to reduce the original problem of determining a function value of sine or cosine to a similar problem in the domain \([0,2\pi]\). After that you can use mirror symmetry to reduce the original problem of determining a function value of sine or cosine to a similar problem in the domain \([0,\tfrac{1}{2}\pi]\) (or even \([0,\tfrac{1}{4}\pi]\) if you wish).
Finally, we introduce three functionsthat are related to the sine, cosine and tangent, and that you may encounter in textbooks.
sec, csc and cot The secant \(\mathrm{sec}\) is the reciprocal of the cosine, the cosecans \(\mathrm{csc}\) is the reciprocal of the sine and the cotangent \(\mathrm{cot}\) is the reciprocal of the tangent. In formula language: \[\mathrm{sec}\,x=\frac{1}{\cos x},\quad \mathrm{csc}\,x=\frac{1}{\sin x}, \quad \mathrm{cot}\,x=\frac{1}{\tan x}\tiny.\]
Mathcentre video
Trigonometric Functions (16:10)


