Goniometrische functies en hun inversen: Goniometrische functies
 Basiseigenschappen van goniometrische functies
Basiseigenschappen van goniometrische functies
Eigenschappen van goniometrische functies Enkele eigenschappen van de goniometrische functies volgen bijna rechtstreeks uit de definities.
Basisregel
Voorbeeld
\[\begin{aligned}\cos^2(\tfrac{1}{6}\pi)+\sin^2(\tfrac{1}{6}\pi) &= \left(\tfrac{1}{2}\sqrt{3}\right)^2+\left(\tfrac{1}{2}\right)^2\\[0.25cm] &= \tfrac{3}{4}+\tfrac{1}{4}= 1\end{aligned}\]
Periodiciteit
Voorbeelden
\[\begin{aligned}\sin(\tfrac{7}{3}\pi) &= \sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(-\tfrac{2}{3}\pi) &= \cos(\tfrac{4}{3}\pi)\\[0.25cm] \tan(-\tfrac{1}{3}\pi) &= \tan(\tfrac{2}{3}\pi)\end{aligned}\]
Spiegelsymmetrie
- Spiegeling om de horizontale as leidt tot: \[\begin{aligned} \sin(-\alpha)&=-\sin(\alpha)\\[0.25cm] \cos(-\alpha)&=\cos(\alpha)\\[0.25cm] \tan(-\alpha)&=-\tan(\alpha)\end{aligned}\]
- Spiegeling om de verticale as leidt tot: \[\begin{aligned}\sin(\pi-\alpha)&=\sin(\alpha)\\[0.25cm] \cos(\pi-\alpha)&=-\cos(\alpha)\\[0.25cm] \tan(\pi-\alpha)&=-\tan(\alpha)\end{aligned}\]
- Spiegeling om de schuine lijn \(y=x\) leidt tot \[\begin{aligned}\sin(\tfrac{1}{2}\pi-\alpha)&=\cos(\alpha)\\[0.25cm] \cos(\tfrac{1}{2}\pi-\alpha)&=\sin(\alpha)\\[0.25cm] \tan(\tfrac{1}{2}\pi-\alpha)&=\frac{1}{\tan(\alpha)}\end{aligned}\]
Voorbeelden
\[\begin{aligned}\sin(-\tfrac{1}{3}\pi) &= -\sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(-\tfrac{1}{3}\pi) &= \cos(\tfrac{1}{3}\pi)\\[0.25cm] \tan(-\tfrac{1}{3}\pi) &= -\tan(\tfrac{1}{3}\pi)\end{aligned}\]
\(\phantom{abc}\)
\[\begin{aligned}\sin(\tfrac{2}{3}\pi) &= \sin(\tfrac{1}{3}\pi)\\[0.25cm] \cos(\tfrac{2}{3}\pi) &= -\cos(\tfrac{1}{3}\pi)\\[0.25cm] \tan(\tfrac{2}{3}\pi) &= -\tan(\tfrac{1}{3}\pi)\end{aligned}\]
\(\phantom{abc}\)
\[\begin{aligned}\sin(\tfrac{1}{3}\pi) &= \cos(\tfrac{1}{6}\pi)\\[0.25cm] \cos(\tfrac{1}{3}\pi) &= \sin(\tfrac{1}{6}\pi)\\[0.25cm] \tan(\tfrac{1}{3}\pi) &= \frac{1}{\tan(\tfrac{1}{6}\pi)}\end{aligned}\]
Domein en bereik Uit de definitie volgt ook onmiddellijk dat het bereik van de sinus- en cosinusfunctie gelijk is aan het segment [-1,1] en dat het domein bestaat uit alle reële getallen. Het bereik van de tangensfunctie bestaat uit alle reële getallen en het domein uit alle reële getallen behalve de getallen die gelijk zijn aan \(\tfrac{1}{2}\pi\) modulo \(\pi\).
Speciale functiewaarden Enkele domeinwaarden hebben speciale waarden voor de sinus-, cosinus- en tangensfunctie die je uit het hoofd moet kennen, dan wel in een mum van tijd en inspanning kunt afleiden met m.bv. de stelling van Pythagoras:
\[
\begin{array}{r|ccccc}
\alpha & 0 & \tfrac{1}{6}\pi & \tfrac{1}{4}\pi & \tfrac{1}{3}\pi & \tfrac{1}{2}\pi
\\ \hline &&&&& \\
\sin \alpha & 0 & \tfrac{1}{2} & \tfrac{1}{2}\sqrt{2} & \tfrac{1}{2}\sqrt{3} & 1 \\ &&&&& \\
\cos \alpha & 1 & \tfrac{1}{2}\sqrt{3} & \tfrac{1}{2}\sqrt{2} & \tfrac{1}{2} & 0 \\ &&&&& \\
\tan \alpha & 0 & \tfrac{1}{3}\sqrt{3} & 1 & \sqrt{3} & - \\
\end{array}
\]
Stel dat je de functiewaarden \(\sin(\tfrac{1}{6}\pi)\), \(\cos(\tfrac{1}{6}\pi)\) en \(\tan(\tfrac{1}{6}\pi)\) wilt uitrekenen. Dan hoort hierbij een punt \(B\) op de eenheidscirkel dat samen met de oorsprong (aangeduid met de letter \(A\)) en de verticale projectie van \(B\) op de horizontale as (aangeduid met de letter \(C\)) de hoekpunten van een rechthoekige driehoek vormt zoals in onderstaande figuur
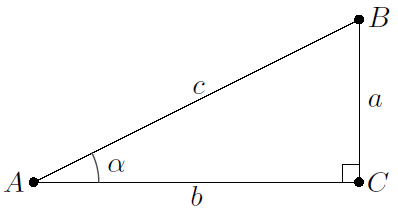
met \(c=1\), \(\alpha=\tfrac{1}{6}\pi\) en \(a=\dfrac{1}{2}\) (dit laatste volgt uit het gegeven dat je bij spiegeling van de driehoek langs de horizontale zijden een gelijkzijdige driehoek krijgt met zijden van lengte 1). Uit de stelling van Pythagoras volgt dan \(b^2=c^2-a^2=\dfrac{3}{4}\) en dus \(b=\tfrac{1}{2}\sqrt{3}\). Per definitie geldt dan \[\cos(\tfrac{1}{6}\pi) = \tfrac{1}{2}\sqrt{3}, \qquad\sin(\tfrac{1}{6}\pi) =\tfrac{1}{2} \qquad\text{ en }\qquad\tan(\tfrac{1}{6}\pi) = \dfrac{1}{\sqrt{3}}= \tfrac{1}{3}\sqrt{3}\tiny.\]
Exacte-waarden-cirkel Met de symmetrie-eigenschappen en de standaardwaarden kun je dan ook andere speciale functiewaarden uitrekenen. Ze staan in onderstaande exacte-waarden-cirkel.
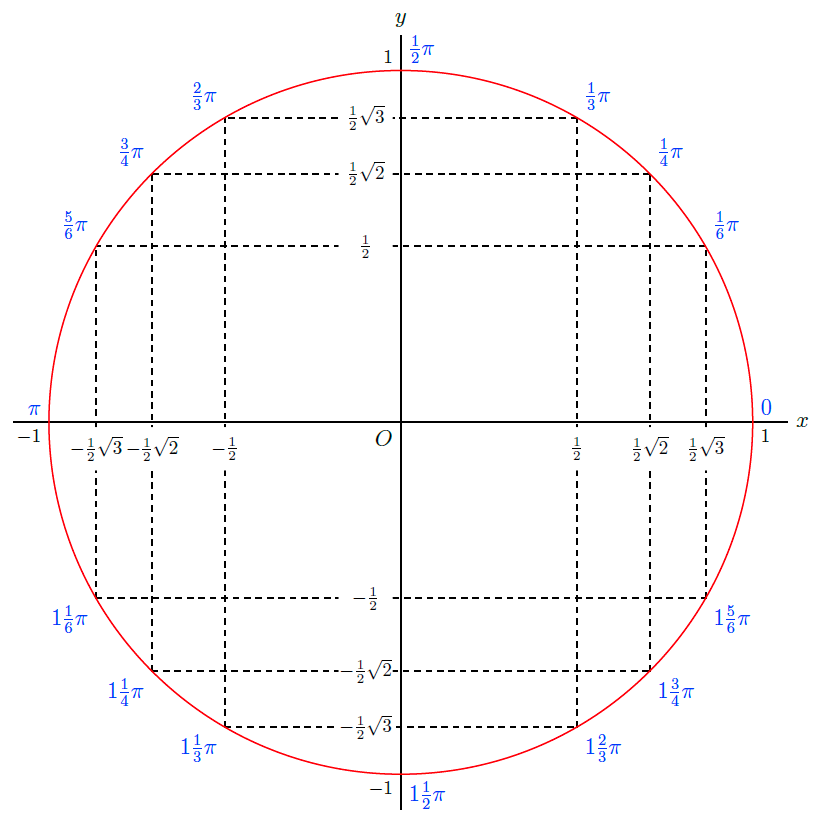
Gegeven \(\sin(\tfrac{1}{3}\!\pi)=\tfrac{1}{2}\!\sqrt{3}\), wat is dan \(\sin(\tfrac{4}{3}\!\pi)\)?
Als \(t=\tfrac{23}{6}\pi\) en we bovenstaande stappen volgen, dan vinden we: \[\begin{array}{rclcl}\cos(\tfrac{23}{6}\pi) &=& \cos(\tfrac{23}{6}\pi-4\pi)\;=\;\cos(-\tfrac{1}{6}\pi)&\phantom{xx}& \blue{\text{periode }2\pi}\\ &=& \cos(\tfrac{1}{6}\pi)&\phantom{xx}& \blue{\text{spiegeling in }x\text{-as}}\\ &=&\tfrac{1}{2}\sqrt{3} &\phantom{xx}& \blue{\text{speciale waarde}}\end{array}\]
Strategie voor het berekenen van goniometrische functiewaarden Voor domeinwaarden die niet binnen \([0,2\pi]\) liggen, gebruik je dus eerst het periodieke gedrag van de goniometrische functies om de bepaling van een functiewaarde van sinus of cosinus terug te brengen tot een probleem op het domein \([0,2\pi]\). Hierna kun je spiegelsymmetrie toepassen om de bepaling van een functiewaarde terug te brengen tot een probleem op het domein \([0,\tfrac{1}{2}\pi]\) (of zelfs tot \([0,\tfrac{1}{4}\pi]\) als je dat zou willen).
Tot slot introduceren we nog drie functies die gerelateerd zijn met de sinus, cosinus en tangens, en die je in handboeken tegen kunt komen.
sec, csc en cot De secans (\(\mathrm{sec}\)) is de reciproke van de cosinus, de cosecans (\(\mathrm{csc}\)) is de reciproke van de sinus en de cotangens (\(\mathrm{cot}\)) is de reciproke van de tangens. In formuletaal: \[\mathrm{sec}\,x=\frac{1}{\cos x},\quad \mathrm{csc}\,x=\frac{1}{\sin x}, \quad \mathrm{cot}\,x=\frac{1}{\tan x}\tiny.\]
Mathcentre video
Trigonometric Functions (16:10)


