Goniometrische functies en hun inversen: Goniometrische functies
 Transformaties van goniometrische functies
Transformaties van goniometrische functies
We hebben al gezien dat standaard sinus- en cosinusfunctie getransformeerd kunnen worden naar andere periodieke functies. We gaan er hier meer systematisch op in.
Verticale verschuiving
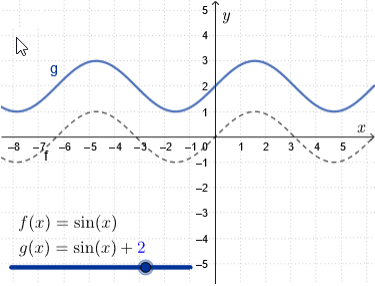
We verschuiven de grafiek van \(f(x)=\sin(x)\) verticaal omhoog met \(\blue{d}\).
De nieuwe functie wordt \[g(x)= \sin(x)+\blue{d}\] De amplitude en de periode blijven gelijk, maar je krijgt nu een evenwichtsstand gelijk aan \(\blue{d}\).
Horizontale verschuiving
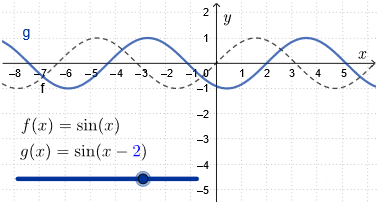
We verschuiven de grafiek van \(f(x)=\sin(x)\) horizontaal naar rechs met \(\blue{c}\).
De nieuwe functie wordt \[g(x)= \sin(x-\blue{c})\] De amplitude, periode en evenwichtsstand blijven gelijk, maar je krijgt nu een verschoven sinusgrafiek. Op het interval \((\blue{c},\blue{c}+2\pi)\) loopt de grafiek dan naar rechts net als de grafiek van de sinusfunctie op het interval \((0,2\pi)\).
Horizontale schaling
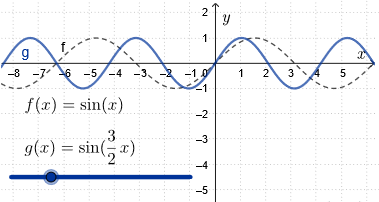
We vermenigvuldigen de grafiek van \(f(x)=\sin(x)\) t.o.v. de \(y\)-as met \(\frac{1}{\blue{b}}\) voor zekere \(\blue{b}\neq 0\).
De nieuwe functie wordt \[g(x)= \sin(\blue{b}\,x)\] De amplitude en de evenwichtsstand blijven gelijk, maar de periode is nu gelijk aan \(\frac{2\pi}{|\blue{b}|}\).
Verticale schaling
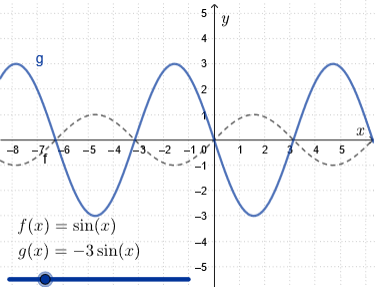
We vermenigvuldigen de grafiek van \(f(x)=\sin(x)\) t.o.v. de \(x\)-as met \(\blue{a}\).
De nieuwe functie wordt \[g(x)= \blue{a}\sin(x)\] De periode en de evenwichtsstand blijven gelijk, maar de amplitude is nu gelijk aan \(|\blue{a}|\).
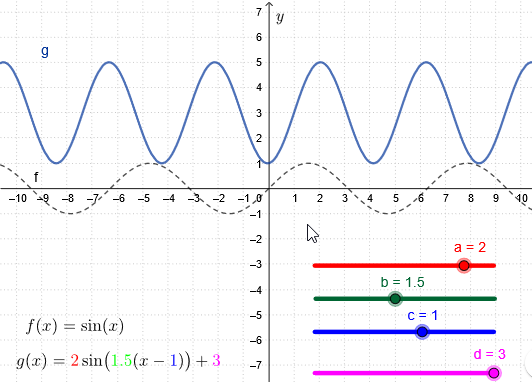
Interactief voorbeeld Je kunt bovengenoemde transformatie combineren en zo elke sinusoïde, d.w.z. een functie van onderstaande vorm, construeren. In onderstaand interactief voorbeeld kun je het effect van de parameters \(a\), \(b\), \(c\) en \(d\) exploreren die de grafiek van de functie \[g(x)=\color{red}{a}\cdot\sin\bigl(\color{green}{b}\cdot(x-\blue{c})\bigr)+\color{magenta}{d}\] opleveren via de schuifbalken.
Identificatie van de parameters van een sinusoïde op basis van een grafiek Als de grafiek van een sinusoïde \(f\) als functie van tijd \(t\) gegeven is kunnen de parameters in de formule \[f(t)=a\sin\bigl(b(t-c)\bigr)+d\] als volgt bepaald worden:
- De amplitude \(a\) is de helft van de verticale afstand tussen een maximum en minimum;
- De periode \(T\) is de horizontale afstand tussen twee opeenvolgende maxima, twee opeenvolgende minima, of twee opeenvolgende horizontale posities waarin de grafiek van de functie de evenwichtsstand in stijgende vorm passeert. Dan geldt dat \(b=\frac{2\pi}{T}\);
- Voor de horizontale verschuiving \(c\) kun je kiezen de horizontale coördinaat van een punt waarin de grafiek stijgend door de evenwichtsstand gaat. Meestal kiezen we het eerste positieve punt met deze eigenschap;
- De evenwichtsstand \(d\) is het gemiddelde van de maximale en minimale waarde van de functie.
Bepaal exacte parameters voor de functie passend bij onderstaande figuur (het volstaat om één mogelijke waarde voor de fase \(\varphi\) te geven).
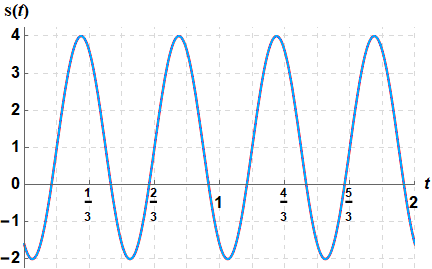
Uit de grafiek lezen we af dat de maximale en minimale waarde gelijk zijn aan respectievelijk \(4\) en \(-2\). De amplitude, zijnde de maximale afwijking van de evenwichtsstand, is gelijk aan de helft van de verticale afstand tussen een maximum en minimum, en in dit geval geldt dus dat \(A=\frac{4-(-2)}{2}=\frac{6}{2}=3\).
De evenwichtsstand \(E\) is het gemiddelde van de maximale en minimale waarde van de functie en in dit geval dus gelijk aan \(\frac{4+(-2)}{2}=\frac{2}{2}=1\).
De periode \(T\) is de horizontale afstand tussen twee opeenvolgende horizontale posities waarin de functiewaarde gelijk is aan \(E\) en de functie stijgend is. In dit geval lezen we af dat dit gebeurt bij \(t=\frac{1}{6}\) en \(t=\frac{2}{3}\). Dus: \(T= \frac{2}{3}-\frac{1}{6}=\frac{1}{2}\). Dan geldt: \(\omega=\frac{2\pi}{T}=\frac{2\pi}{\frac{1}{2}}=4\pi\).
Om de fase te bepalen herschrijven we de sinusoïde eerst in de vorm \(A\sin\bigl(\omega\,(t-c)\bigr)+E\) omdat we de parameter \(c\) gemakkelijk kunnen aflezen uit de grafiek: het is namelijk de horizontale coördinaat van een punt waarin de grafiek stijgend door de evenwichtsstand gaat. Als we het eerste positieve punt met deze eigenschap kiezen, dan is \(c=\tfrac{1}{6}\). Hieruit volgt dat \(\varphi=-\omega\cdot c=-4\pi\times \tfrac{1}{6}=-\tfrac{2}{3}\pi\).
Samengevat: \[\begin{aligned}f(t)&=1+3\sin\bigl(4\pi\,(t-\tfrac{1}{6})\bigr)\\[0.25cm] &=1+3\sin(4\pi\,t-\tfrac{2}{3}\pi)\end{aligned}\] Bedenk wel dat de fase niet uniek is maar modulo \(2\pi\) gekozen kan worden. Als je bijvoorbeeld \(c=\tfrac{2}{3}\) had gekozen als de horizontale coördinaat van een punt waarin de grafiek stijgend door de evenwichtsstand gaat, dan was het resultaat voor de fase \(\varphi=-2\pi\times \tfrac{2}{3}=-\tfrac{8}{3}\pi=-\tfrac{2}{3}\pi-2\pi\) geweest.