Exponential growth model

Unlimited growth: Exponential growth

Exponential growth model

Properties of exponential growth For exponential growth of a quantity \(y(t)\) at time \(t\) :

the quantity \(y(t)\) is multiplied with the same number per unit of time, the growth factor per unit of time;
\(y(t)\) can be described by an exponential function \(y(t)=c\cdot g^t\), in which \(g\) is the growth factor per unit of time and \(c\) the value of quantity \(y(t)\) at time \(t=0\). Since we will always assume that \(c\) represents an initial quantity, we therefore assume \(c>0\);
the corresponding \((y,t)\)-graph is an increasing function when \(g>1\) and a decreasing function when \(0<g<1\);
the relative growth rate \(\displaystyle\frac{y'(t)}{y(t)}\) is constant. This can also be formulated as follows: the derivative of the quantity \(y'(t)\) is a multiple of the quantity \(y(t)\) at that same moment in time, that is \[y'(t)=r\cdot y(t)\] This relationship between a function and its derivative is also called the differential equation of exponential growth and \(r\) is called the relative growth rate.

Relation between r and g Note that because the derivative of \(y(t)=c\cdot g^t\) is given by \(y'(t)=c\cdot \log(g) \cdot g^t\), the relative growth rate can be expressed as \[ r =\frac{y'(t)}{y(t)} = \frac{c\cdot \ln(g)\cdot g^t}{c \cdot g^t} =\ln(g)\]

Exponential decay If \(0<g<1\), or equivalently \(r<0\), the name exponential decay is used.

Using percentages Instead of the growth factor per unit of time, sometimes simply abbreviated as "growth factor", the increase or decrease per unit of time in terms of percentage is also used. Then we speak of a growth percentage per unit of time.

A change of \(p\mathrm{\%}\) per unit of time is equivalent to an exponential growth factor of \(\displaystyle g=1+\frac{p}{100}\).
Similarly, a growth factor of \(g\) per unit of time is equivalent to a change in terms of percentage of \(p=(g-1)\cdot 100\mathrm{\%}\).

An annual decrease of \(7.5\mathrm{\%}\) corresponds to \(p=-7.5\), so the growth factor is \(\displaystyle g=1+\frac{-7.5}{100}=0.925\) annually.
A growth factor of \(0.975\) corresponds to a change in terms of percentage of \(p=(0.975-1)\cdot 100\mathrm{\%}=-2.5\mathrm{\%}\), so a decrease \(2.5\mathrm{\%}\).

The first three characterisations of exponential growth you may know already. We will practice them a bit more in this chapter. The differential equation is probably new. But whichever approach is chosen, everything fits together nicely.

The differential equation of exponential growth can be solved explicitly, i.e., an explicit formula for \(y(t)\) can be determined. This provides the relationship between the first and last property of exponential growth, namely that growth factor \(g\) equals \(e^r\), or in other words, that the relative growth rate constant \(r\) equals \(\ln(g)\).

The general solution of the differential equation of exponential growth \[y'(t)=r\cdot y(t)\] is equal to \[y(t)=c\cdot e^{r\cdot t}\] for some constant \(c\).

If \(r<0\), we speak of exponential decay and \(y\) approaches the value of \(0\) for big time \(t\). If \(r>0\), then \(y\) "explodes" with increasing time. The following dynamic figure illustrates this for \(y(t)=e^{r\,t}\).

GeoGebra

For math enthusiasts, we give the proof of the assertion that \(y(t)=c\cdot e^{r\cdot t}\) is the general solution of the differential equation \(y(t)=r\cdot y(t)\).
In this proof we use the following lemma: if \(f'(t)=0\) a certain function \(f(t)\), then \(f(t)\) is a constant function.
Suppose \(y(t)\) is a solution of the differential equation of exponential growth, ie has the property \[y'(t)=r\cdot y(t).\] Then, we have: \[y'(t)-r\cdot y(t)=0\] Multiply now both sides of the equation with \(e^{-r\cdot t}\): \[\bigl(y'(t)-r\cdot y(t)\bigr)\cdot e^{-r\cdot t}=0\] Expand the left hand side: \[y'(t)\cdot e^{-r\cdot t} - r\cdot y(t)\cdot e^{-r\cdot t}=0\] At the left-hand side we can now recognize the product rule of differentiation: \[\bigl(y(t)\cdot e^{-r\cdot t}\bigr)'= 0\] From the lemma it follows that: \[\bigl(y(t)\cdot e^{-r\cdot t}\bigr)= c\] for certain constant \(c\). But this means \[y(t)= c\cdot e^{r\cdot t}\]
This is what had to be proved!

Microbial growth of Escherichia coli (E. coli) bacteria proceeds fast: every 20 minutes the number of bacteria doubles, as we have seen at the beginning of exponential growth. Starting from 1 coli bacteria at time \(t=0\), there are 2 bacteria after 20 minutes, 4 bacteria after 40 minutes and 8 bacteria after 60 minutes. The growth factor \(g\) per hour is equal to 8. This might seem not such a strong growth at a first glance, but look at the table below.

\[\begin{array}{|l|l|} \hline
\text{Time } (\textit{uours}) & \text{Number of bacteria} \\ \hline
0 & 1 \\
1 & 8 \\
2 & 64 \\
3 & 512 \\
4 & 4\,096 \\
5 & 32\,768 \\
6 & 261\,144 \\
7 & 2\,097\,152 \\
8 & 16\,777\,216 \\ \hline \end{array}\]

After 8 hours roughly 17 million bacteria have emerged through cell division from one single bacterium! The graph below illustrates the enormous increase of the number of bacteria.

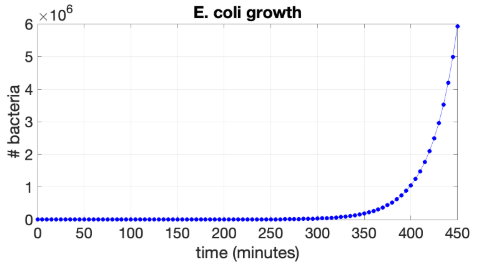
The relative growth rate constant per hour is equal to the logarithm of the growth factor, in this case \(\ln(8)\;\mathrm{hour}^{-1}\).
The formula for the number of bacteria at time \(t\) (in hours) can also be written as \(N(t)=8^t = e^{(\ln(8)\cdot t)}\approx e^{(2.07944\cdot t)}\) or as \(N(t)=10^{(\log_{10}(8)\cdot t)}\approx 10^{(0.90309\cdot t)}\).

With this formula we can calculate the number of bacteria at any time, but also at what time a certain number of bacteria is reached. For example, to calculate when with the given exponential growth there are 1 billion bacteria, we have to solve the equation \(8^t=10^9\). This is equivalent to the problem \(10^{(\log_{10}(8)\cdot t)}=10^9\), or \(\log_{10}(8)\cdot t=9\). So \(\displaystyle t=\frac{9}{\log_{10}(8)}\approx 9.97\;\mathrm{hours}\). After approximately 10 hours there are 1 billion bacteria!