Onbegrensde groei: Exponentiële groei
 Exponentieel groeimodel
Exponentieel groeimodel
Eigenschappen van exponentiële groei Bij exponentiële groei van een grootheid \(y(t)\) op tijdstip \(t\):
- wordt de grootheid per tijdseenheid met hetzelfde getal, de groeifactor per tijdseenheid, vermenigvuldigd;
- hoort een formule van de vorm \(y(t)=c\cdot g^t\), waarin \(g\) de groeifactor per tijdseenheid is en\(c\) de waarde van de grootheid op tijdstip \(t=0\), waarbij we altijd zullen veronderstellen dat \(c\) een beginhoeveelheid voorstelt en dat dus \(c>0\);
- is de bijpassende \((y,t)\)-grafiek een toenemend stijgende functie als \(g>1\) en een afnemend dalende functie als \(0<g<1\);
- is de relatieve groeisnelheid \(\displaystyle\frac{y'(t)}{y(t)}\) constant. Dit kan ook geformuleerd als dat afgeleide van de grootheid een veelvoud van de grootheid op hetzelfde moment, d.w.z. \[y'(t)=r\cdot y(t)\] Dit verband tussen afgeleide en functie noemen we ook wel de differentaalvergelijking van exponentiële groei en hierbij heet \(r\) de relatieve groeisnelheidsconstante.
In plaats van de groeifactor per tijdseenheid, ook wel simpelweg afgekort met 'groeifactor', wordt ook wel de procentuele toename of procentuele afname per tijdseenheid gebruikt. We spreken dan van een groeipercentage per tijdseenheid.
Bij een verandering van \(p\mathrm{\%}\) per tijdseenheid hoort exponentiële groei met groeifactor \(\displaystyle g=1+\frac{p}{100}\).
Bij de groeifactor \(g\) per tijdseenheid hoort een verandering van \(p=(g-1)\cdot 100\mathrm{\%}\).
Bij een jaarlijkse afname van \(7.5\mathrm{\%}\) is \(p=-7.5\) en is de groeifactor \(\displaystyle g=1+\frac{-7.5}{100}=0.925\) per jaar.
Omgekeerd hoort bij een groeifactor van \(0.975\) een procentuele verandering van \(p=(0.975-1)\cdot 100\mathrm{\%}=-2.5\mathrm{\%}\), dus een afname van \(2.5\mathrm{\%}\).
De eerste drie karakteriseringen van exponentiële groei zullen we in dit hoofdstuk oefenen; nieuw is het stukje differentiaalvergelijking. Maar welke invalshoek ook gekozen wordt, alles hangt mooi samen.
De differentiaalvergelijking van exponentiële groei kan opgelost worden, d.w.z. een expliciete formule voor \(y(t)\) kan bepaald worden. Dit levert het verband tussen de eerstgenoemde en de laatstgenoemde eigenschap van exponentiële groei op, namelijk dat groeifactor \(g=e^r\), oftewel de relatieve groeisnelheidsconstante is \(r=\ln(g)\).
De algemene oplossing van de differentiaalvergelijking van exponentiële groei \[y'(t)=r\cdot y(t)\] is gelijk aan \[y(t)=C\cdot e^{r\cdot t}\] voor zekere constante \(C\).
Als \(r<0\), dan is er sprake van exponentieel verval en nadert de waarde van \(y\) de waarde \(0\) voor grote tijd \(t\). Als \(r>0\), dan 'explodeert' de oplossing juist naarmate de tijd toeneemt. Onderstaande dynamische figuur illustreert dit voor \(y(t)=e^{r\,t}\).
Microbiële groei van Escherichia coli (E. coli) bacteriën gaat snel: elke 20 minuten verdubbelt het aantal bacteriën. Uitgaande van 1 bacterie op het starttijdstip \(t=0\) zijn er na 20 minuten dus 2 bacteriën, na 40 minuten 4 bacteriën en na 60 minuten 8 bacteriën. De groeifactor per uur is dus gelijk aan 8. Dit lijkt op het eerste gezicht misschien niet zo'n sterke groei, maar kijk in onderstaande tabel wat er gebeurt. De berekening kun je doen met de formule \(N(t)=8^t\), met tijd \(t\) in uren.
\[\begin{array}{|l|l|} \hline
\text{Tijd } (\textit{uren}) & \text{Aantal bacteriën} \\ \hline
0 & 1 \\
1 & 8 \\
2 & 64 \\
3 & 512 \\
4 & 4\,096 \\
5 & 32\,768 \\
6 & 261\,144 \\
7 & 2\,097\,152 \\
8 & 16\,777\,216 \\ \hline \end{array}\]
Na 8 uur zijn door celdeling uit 1 bacterie bij exponentiële groei pakweg 17 miljoen bacteriën ontstaan. Onderstaande grafiek illustreert de enorme toename van het aantal bacteriën.
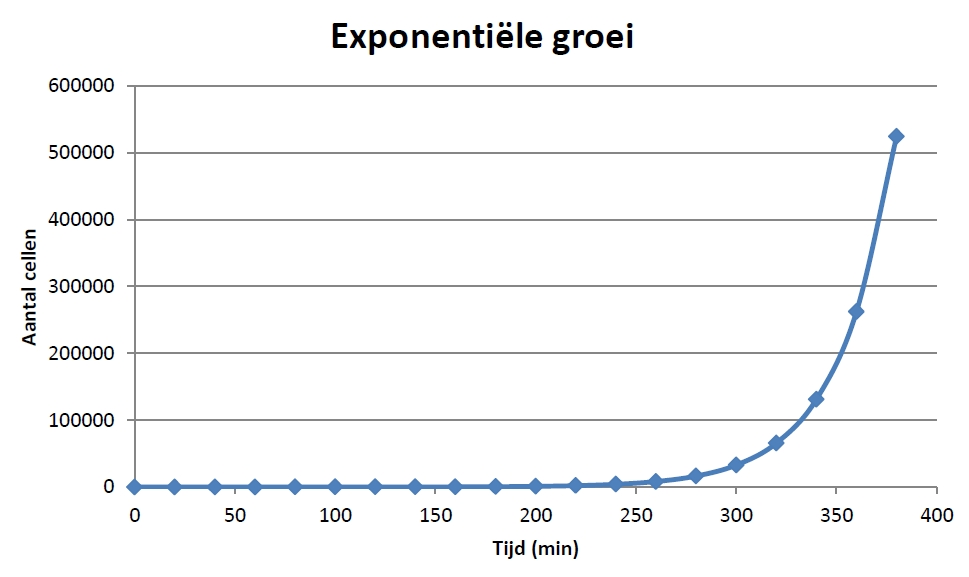
De relatieve groeisnelheidsconstante per uur is gelijk aan de logaritme van de groeifactor, in dit geval \(\ln(8)\;\mathrm{uur}^{-1}\).
De formule voor het aantal bacteriën op tijdstip \(t\) (in uren) kan ook opgeschreven worden als \(N(t)=e^{(\ln(8)\cdot t)}\approx e^{(2.07944\cdot t)}\) of als \(N(t)=10^{(\log_{10}(8)\cdot t)}\approx 10^{(0.90309\cdot t)}\).
Met zo'n formule in de hand kun je het aantal bacteriën op elk tijdstip uitrekenen, maar ook bepalen op welk tijdstip een bepaald aantal bacteriën bereikt wordt. Bijvoorbeeld, om uit te rekenen wanneer bij de gegeven exponentiële groei 1 miljard bacteriën ontstaan zijn, los je de vergelijking \(8^t=10^9\) op. Dit is equivalent met het probleem \(10^{(\log_{10}(8)\cdot t)}=10^9\), oftewel \(\log_{10}(8)\cdot t=9\). Dus \(\displaystyle t=\frac{9}{\log_{10}(8)}\approx 9.97\;\mathrm{uur}\). Na pakweg 10 uur is het aantal van 1 miljard bereikt!


