Onbegrensde groei: Exponentiële groei
 Meetkundige "oplossing" via een lijnelementenveld
Meetkundige "oplossing" via een lijnelementenveld
Dynamisch systeem De differentiaalvergelijking van exponentiële groei is een voorbeeld van een dynamisch systeem, d.w.z. een differentiaalvergelijking met tijd als enige onafhankelijke variabele. Een dynamisch systeem dat geschreven kan worden als eerste-orde differentiaalvergelijking in de vorm \[\frac{\dd y}{\dd t}=\varphi(t,y)\] waarbij \(\varphi\) een of andere functie in twee veranderlijken is, kan op de volgende meetkundige manier “opgelost” worden.
Lijnelementenveld Neem een punt \((a,b)\) en veronderstel dat er een oplossing \(y(t)\) van de differentiaalvergelijking is die door \((a,b)\) gaat. Er geldt voor deze functie \(y\) dat \[y(a)=b\] en dat \[y'(a)=\frac{\dd y}{\dd t}(a)=\varphi\bigl(a,y(a)\bigr)=\varphi(a,b)\] De raaklijn aan de grafiek van \(y\) in het punt \(a,b\) is door deze twee getallen geheel bepaald. Deze raaklijn heeft immers de vergelijking \[y=b+\varphi(a,b)\cdot(t-a).\] De functie \(y\) zelf is onbekend, maar de raaklijn van \(y\) door \((a,b)\) wel. Als je nu in het punt \((a,b)\) een klein stukje van die raaklijn tekent, dan zal dat lijnstukje goed lijken op de oplossing die door \((a,b)\) gaat. Zo'n lijnstukje heet een raaklijnelement of kortweg lijnelement in een punt van het \(t,y\)-vlak. Vervolgens kan je voor veel verschillende punten \((a,b)\) in het \(t,y\)-vlak de lijnelementen tekenen. Een tekening met een aantal lijnelementen heet een lijnelementenveld of hellingsveld van de differentiaalvergelijking. Door nu een vloeiende kromme te tekenen die in elk punt raakt aan de lijnelementen krijg je een zogenaamde integraalkromme, de grafiek dus van een oplossing van de differentiaalvergelijking. Zonder te rekenen kan je op deze manier vaak al een idee krijgen van de vorm van de grafiek van de oplossingen van de differentiaalvergelijking en inzien hoe oplossingen zich na verloop van tijd gedragen. We zullen het lijnelementenveld ook gebruiken om in te zien hoe oplossingen zich gedragen bij dynamische systemen van begrensde groei.
Lijnelementenvelc bij exponentieel verval Hieronder staat het lijnelementenveld getekend voor de differentiaalvergelijking \(\displaystyle\frac{\dd y}{\dd t}=r\cdot y\) met \(r=-0.7\) (dus \(\varphi(t,y)=-0.7y\)). Ook zijn twee integraalkrommen in de figuur opgenomen. Het valt misschien op dat bij alle punten op een horizontale lijn steeds de lijnelementen dezelfde richting hebben: dit komt omdat het rechterlid niet van tijd afhangt. Als je een oplossingskromme schetst door lijnen in het lijnelementenveld te volgen, dan zie je in dat elke oplossing na verloop van tijd nadert tot de evenwichtsoplossing \(y=0\).
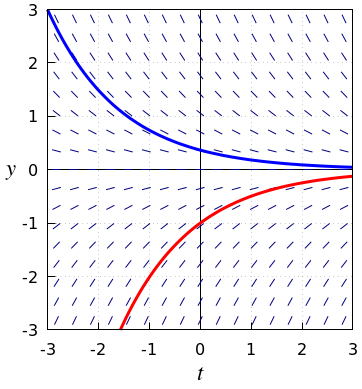
Een lijnelementenveld van een gegeven differentiaalvergelijking van eerste orde en integraalkrommen berekend met een numeriek methode geven vaak een goede indruk van hoe oplossingen er uit zien en wat voor gedrag zij vertonen. In veel praktijkgevallen is er ook niet veel meer mogelijk dan numerieke berekeningen, al dan niet in combinatie met kwalitatieve methoden die alleen maar een globale indruk van het gedrag van oplossingen geven.
Interactieve versie van het lijnelementenveld Voor wie nieuwsgierig is: Je kunt alvast spelen met onderstaande interactieve versie van het lijnelementenveld bij een differentiaalvergelijking. Als voorbeeld is de differentiaalvergelijking van logistische groei klaargezet met een sigmoïde als voorbeeld van één van de vele mogelijke oplossingskrommen. Dit groeimodel bespreken we later nog. Door het punt \(P\) te verslepen zie je verschillende oplossingskrommen. Dit interactieve diagram bevat ook een verplaatsbare 'cursor' die op elke positie een bijpassend lijnelement laat zien


