Kinetiek van IV bolusinjectie van propranolol Onderstaande schermafdruk van een computerprogramma toont de tabel en de grafiek van de gemeten plasmaconcentratie van een proefpersoon in deze studie Het tijdstip \(t=0\) is gelijk gekozen aan het moment dat de toediening van propranolol gestopt is en meetwaarden zijn na enkele uren bepaald. Ook is in deze figuur een geslaagde benadering van het concentratieverloop met een wiskundige functie te zien. Hoe men aan dergelijke wiskundige benaderingen komt zal duidelijk worden in deze sectie.

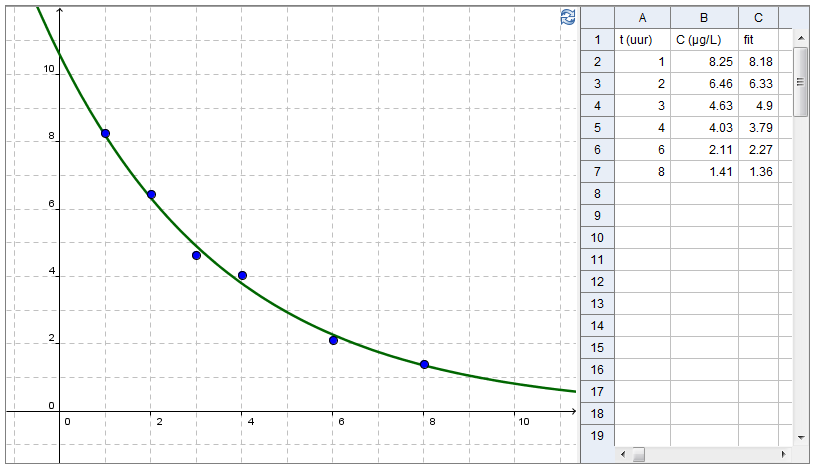
Via een aantal vereenvoudigingen komt men tot een wiskundig model voor het verloop van de plasmaconcentratie.

Een open 1-compartimentmodel Beschouw, om te beginnen, het menselijk lichaam als één systeem waaraan het medicijn toegediend kan worden en waaruit het medicijn ook weer kan verdwijnen (bijvoorbeeld door metabolisme in organen en via uitscheiding in de vorm van urine). Dit heet een open, 1-compartimentmodel: “open” omdat een farmacon, d.w.z. het werkend bestanddeel van een medicijn, geabsorbeerd of geëlimineerd kan worden door het lichaam en “1-compartimentmodel” omdat het menselijk lichaam als één geheel beschouwd wordt en niet in verschillende deelsystemen opgesplitst is. Met andere woorden, in dit model negeert men de wijze waarop het farmacon over het lichaam gedistribueerd wordt in bloedplasma, weefselvocht, en organen; men bekijkt alleen het zogenaamde centrale compartiment.

Laat \(C(t)\) de concentratie van een geneesmiddel zijn op tijdstip \(t\) nadat het medicijn snel ingespoten is in een bloedader en zich razendsnel verdeeld heeft in het lichaam, zo snel dat men mag veronderstellen dat op tijdstip \(t=0\) de maximale plasmaconcentratie van het medicijn aanwezig is in het lichaam. In farmacologie spreekt men ook wel van een IV Bolusinjectie.

Kinetiek volgens een open 1-compartimentmodel Het gebruik van een 1-compartimentmodel impliceert ook dat men veronderstelt dat de verdeling van het farmacon over bloedplasma en andere delen van het lichaam razendsnel plaats vindt zodat er steeds sprake is van een evenwicht, ook al wordt het farmacon steeds geëlimineerd uit het lichaam. Het farmacon verdeeld zich in dit model over een schijnbaar volume van het compartiment, het zogenaamde verdelingsvolume \(V_d\). Als \(D(t) \) de op tijdstip \(t\) nog in het lichaam aanwezige dosis is, dan geldt dus de gelijkheid \[D(t)=V_d\cdot C(t)\] Neem nu aan dat de mate van eliminatie van het farmacon evenredig is met de heersende plasmaconcentratie: \[D'(t)=-\mathrm{Cl}\cdot C(t),\] waarbij \(\mathrm{Cl}\) de totale lichaamsklaring (clearance) van een farmacon, kortweg klaring, is. De eenheid van klaring is dus volume per tijdseenheid (L/h, mL/min, etc.), maar klaring wordt in tabellen (zie bijvoorbeeld www.cbg-meb.nl en www.geneesmiddelenrepertorium.nl) vaak genoteerd als het aantal liter per tijdseenheid per 70 kg lichaamsgewicht. Vanwege het verband tussen dosis en plasmaconcentratie kan ook alles in termen van de concentratie \(C(t)\) opgeschreven worden; dit leidt tot de volgende differentiaalvergelijking: \[C'(t)=-k\cdot C(t),\] waarbij er dus sprake is van eerste-orde kinetiek met eliminatiesnelheidsconstante \(k\). De eliminatiesnelheidsconstante is dus gelijk aan \[k=\frac{\mathrm{Cl}}{V_d}.\] Schematisch wordt dit 1-compartimentmodel ook vaak als volgt weergegeven:

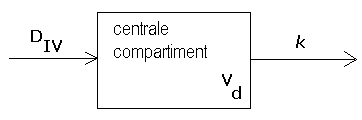
Elk compartiment wordt door een rechthoek gerepresenteerd: in dit geval is er maar één compartiment, het centrale compartiment, maar in veel modellen worden meerdere compartimenten gebruik (bijvoorbeeld om onderscheid te maken tussen het centrale compartiment en het perifere weefsel). De pijlen geven aan hoe stoffen door een compartiment geabsorbeerd en geëlimineerd worden. De wiskundige modellering van deze processen wordt bij de pijlen summier aangegeven: \(D_\mathrm{IV}\) staat voor een eenmalige intraveneuze bolusinjectie met dosis \(D\) en de letter bij de uitgaande pijl in bovenstaand diagram representeert een eliminatie volgens 1ste orde kinetiek met eliminatiesnelheidsconstante \(k\). In een compartiment geeft men soms ook expliciet aan dat een verdelingsvolume \(V_d\) van het farmacon een rol speelt.

Formules bij eerste-orde farmacokinetiek De oplossing van differentiaalvergelijking \[C'(t)=-k\cdot C(t)\] is gelijk aan \[C(t)=C_0\cdot e^{-kt}\] In het voorbeeld van propranolol zijn de parameters \(c_0\) en \(k\) op basis van de meetgegevens via een functiefit (wiskundigen spreken liever van de methode van regressie) geschat.

I.p.v. de eliminatiesnelheidsconstante \(k\) wordt vaak een halveringstijd \(t_{1/2}\) van een farmacon gehanteerd: dit is de tijd waarin de concentratie halveert. Het volgende verband geldt: \[t_{1/2}=\frac{\ln(2)}{k}\approx \frac{0.693}{k}\] De literatuurwaarde voor de halveringstijd van propranolol is 2.8 uur (Evans et al., 1973)

Literatuur

Evans, G.H, Nies, A.S., & Shand, D.G. (1973). The disposition of propranolol. III. Decreased half-time and volume of distribution as a result of plasma binding in man, monkey, dog and rat. The Journal of Pharmacology and Experimental Therapeutics, 186(1), 114-122.

Fagan, T.C, Walle, T., Walle, U.K., Conradi, E.C, Harmon, G., & Gaffney, T.E. (1982). Early Kinetics of Intravenous Propranolol. British Journal of Clinical Pharmacology 13, 571-574.

Stapleton, M.P. (1997). Sir James Black and Propranolol. The role of the Basic Sciences in the History of Cardiovascular Pharmacology. Texas Heart Institute Journal, 24(4), 336-342. Online: www.ncbi.nlm.nih.gov/pmc/articles/PMC325477/pdf/thij00027-0106.pdf