Onbegrensde groei: Toepassingen
Ontlading van een condensator
Condensator Elke geleider kan beschouwd worden als een elektrische component voor opslag van elektrische lading of als bron van elektrische lading. We concentreren ons hier op de eerste functie. De hoeveelheid lading per aangelegde spanning heet de capaciteit en wordt gemeten in de eenheid farad (met symbool F, afkomstig van Faraday). Een condensator is een elektrische component met een grote capaciteit.
Een condensator is in traditionele exemplaren opgebouwd uit twee vlakke geleiders met een relatief grote oppervlakte, die zich dicht bij elkaar bevinden en gescheiden zijn door een niet-geleidend materiaal of vacuüm, het diëlektricum. Hieronder is foto van een klassieke vlakke condensator, met lucht en glas als diëlektricum, die voor onderwijsdoeleinden gebruikt werd (bron: Schulhistorische Sammlung Bremerhaven)
Wanneer de ene geleider positief geladen wordt ten opzichte van de andere, verplaatsen de aan moleculen in het diëlektricum gebonden elektronen zich een beetje naar de positief geladen geleider. De naam is afgeleid van het Latijn werkwoord condensare, dat samenpersen betekent en in de context van een plaatcondensator betrekking heeft op de ladingen die samengeperst worden bij de vlakke platen van de condensator.
Symbool voor een condensator Het symbool voor een condensator in een elektrisch circuit symboliseert de opbouw van een vlakke condensator en kent twee varianten, namelijk
In het rechtersymbool wordt voor een gepolariseerde condensator, beter gekend onder de benaming 'elektrolytische condensator' (afgekort: elco), gebruikt die een plus- en minaansluiting heeft, waarbij het gekromde lijnstuk gebruikt wordt als indicatie dat daar negatieve lading zich ophoopt terwijl de andere geleider positief geladen is. Bij het linkersymbool voor een bipolaire condensator maken we geen onderscheid tussen positief of negatief geladen lading. Dit symbool lijkt op dat van een spanningsbron maar bij een condensator zijn de verticale streepjes even lang en even dik.
Oplading van een condensator Stel dat je de polen van een batterij, die een bronspanning \(V\) levert, via een geleidende draad en een schakelaar verbindt met een vlakke condensator; zie onderstaande tekening van de stroomkring.
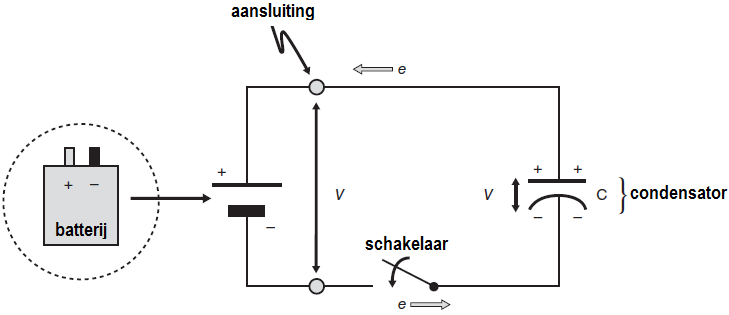Zodra je de schakelaar sluit en een gesloten elektrisch circuit ontstaat, leidt het potentiaalverschil tussen de aansluitingen van de batterij tot een elektrisch veld in de draad waardoor elektronen gaan stromen: de elektronen uit de bovenste plaat van de vlakke condensator stromen naar de positieve aansluiting van de batterij en zorgen er zo voor dat positieve lading op de plaat achterblijft. Het elektrisch veld zorgt tegelijkertijd dat een even groot aantal elektronen van de negatieve aansluiting van de batterij naar de onderste plaat van de condensator gaan en zorgen daar voor een negatieve lading. De oplading van de condensator gaat door totdat een even grote maar tegengestelde lading op beide platen aanwezig is en het potentiaalverschil tussen de platen overeenstemt met de spanning die de batterij levert. Er geldt op dat moment voor de lading \(Q\) op de bovenste condensatorplaat dat \[Q=C\cdot V\] We zullen later het proces van oplading van een condensator meer in detail bekijken. Maar wat opvalt is dat de condensator uiteindelijk weinig stroom doorlaat (alleen maar een lekstroom).
Ontlading van een RC circuit
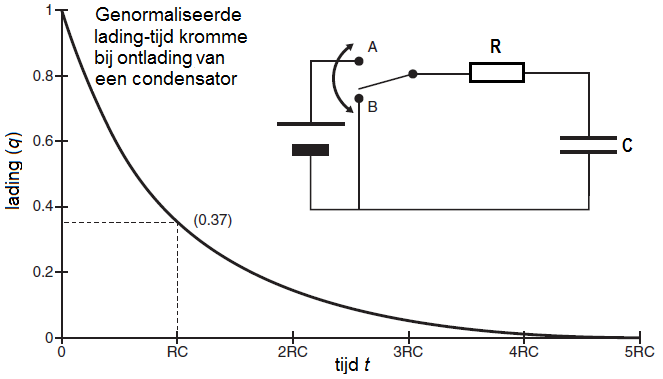
We bekijken een elektrisch circuit waarin een condensator met capaciteit \(C\) ontlaadt via een weerstand \(R\) zoals in het elektrische schema in onderstaand diagram. Eerst stond de schakelaar in stand A zodat de condensator volledig opgeladen kon worden. Hierna wordt de schakelaar in het RC circuit op tijdstip \(t=0\) in positie B gebracht, speelt de batterij geen rol meer, en kan de ontlading van de condensator beginnen, met de condensator functionerend als een continue afnemende spanningsbron
Afleiding van een bijpassende differentiaalvergelijking
Bovenstaande genormaliseerde lading-tijd grafiek kan wiskundig exact beschreven worden. Tijdens het ontladingsproces gelden voor het RC circuit de wetten van Kirchhoff. De spanningswet zegt in dit geval dat de som van het spanningsverlies over de weerstand en over de condensator gelijk is aan nul. In formulevorm: \[V_R+V_C=IR+\frac{Q}{C}=0\] waarbij \(Q(t)\) de lading van de bovenste plaat van de condensator is op tijdstip \(t\) en \(I(t)\) de stroomsterkte in het gesloten circuit is op tijdstip \(t\). De stroomsterkte \(I\) is gelijk aan de hoeveelheid lading die per seconde op ieder moment door het circuit stroomt en is per definitie gegeven door de volgende vergelijking: \[I(t) = Q'(t)\] We hebben dan ook de volgende differentiaalvergelijking: \[R\frac{\dd Q}{\dd t} + \frac{Q}{C} =0\] oftewel: \[\frac{\dd Q}{\dd t} =-\frac{1}{RC}Q\] Dit is de differentiaalvergelijking van exponentieel verval, die geschreven kan worden als \[\frac{\dd Q}{\dd t} = -\frac{Q}{\tau}\] met karakteristieke tijd \(\tau=RC\), ook wel RC-tijd genoemd. De oplossing met \(Q(0)=Q_0\) is \[Q(t)=Q_0e^{{}^{-\frac{t}{\tau}}}\]
Elektrisch analogon voor een ionkanaal in een celmembraan Bovenstaand voorbeeld van een condensator in een elektrisch circuit doet niet meteen denken aan psychobiologie of biomedische wetenschappen, maar heeft er wel degelijk mee te maken: complexe elektrische eigenschappen van een celmembraan worden namelijk inzichtelijk door de membraan met een elektrisch circuit bestaande uit weerstanden, batterijen en condensatoren te vergelijken. Hierbij wordt de isolerende lipidendubbellaag tussen de twee geleidende media van de intra- en extracellulaire vloeistof vergeleken met het diëlektricum van een condensator tussen de twee geleidende platen. Door deze constructie heeft een condensator de capaciteit om lading op te slaan als er over het diëlektricum een elektrisch spanningsverschil wordt aangelegd. Elk ionkanaal correspondeert met een in serie geschakelde batterij en weerstand, zoals in onderstaande figuur gevisualiseerd wordt.
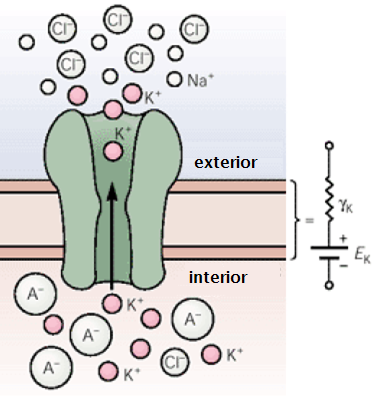
De hele werking van ionkanaal en celmembraan wordt dan gerepresenteerd door een elektrisch circuit zoals in onderstaande figuur. Hierin is \(E_\mathrm{K}\) de Nernstpotentiaal van het ionkanaal op basis van concentratieverschillen binnen en buiten de cel. Conventie in de elektrofysiologie is hierbij om de stroomrichting van positief geladen deeltjes van binnen naar buiten de cel te kiezen. In een plaatje (hier voor het \(\mathrm{K}^{+}\) ion, maar meestal laten we de lading weg en symboliseren alleen de naam van het ion) ziet het elektrische circuit er als volgt uit:
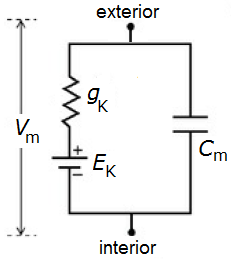
In rust volgt in bovenstaande situatie uit de stroomwet van Kirchhoff dat \(V_m\) gelijk is aan de Nernstpotentiaal \(E_\mathrm{K}\) en dit wordt dan de rustmembraanpotentiaal. Bij aanwezigheid van meer ionkanalen zal de rustmembraanpotentiaal \(V_r\) een gewogen gemiddelde zijn van de Nerstpotentialen van de bijpassende ionkanalen.
Herstel van de rustmembraanpotentiaal als een stimulus stopt Als we \(V=V_m-V_r\) definiëren, dat wil zeggen kijken naar het potentiaalverschil met de rustmembraanpotentiaal, dan krijgen we de volgende differentiaalvergelijking voor de membraanpotentiaal \[I_\mathrm{stim}=C_m\frac{\dd V}{\dd t} + g_\mathrm{\small K} V\] Als de stimulus gelijk aan nul, dan is de differentiaalvergelijking dezelfde als die van een ontladende condensator. Bij een cel die niet in rust is, maar bijvoorbeeld een startwaarde van de spanning \(V_0\) ongelijk aan nul heeft op tijdstip \(t=0\), zal de spanning de oorspronkelijke rustmembraanpotentiaal naderen via een exponentieel verval proces volgens de formule \[V(t)=V_0\cdot e^{-\frac{ g_\mathrm{\small K}}{C_m}t}\]
