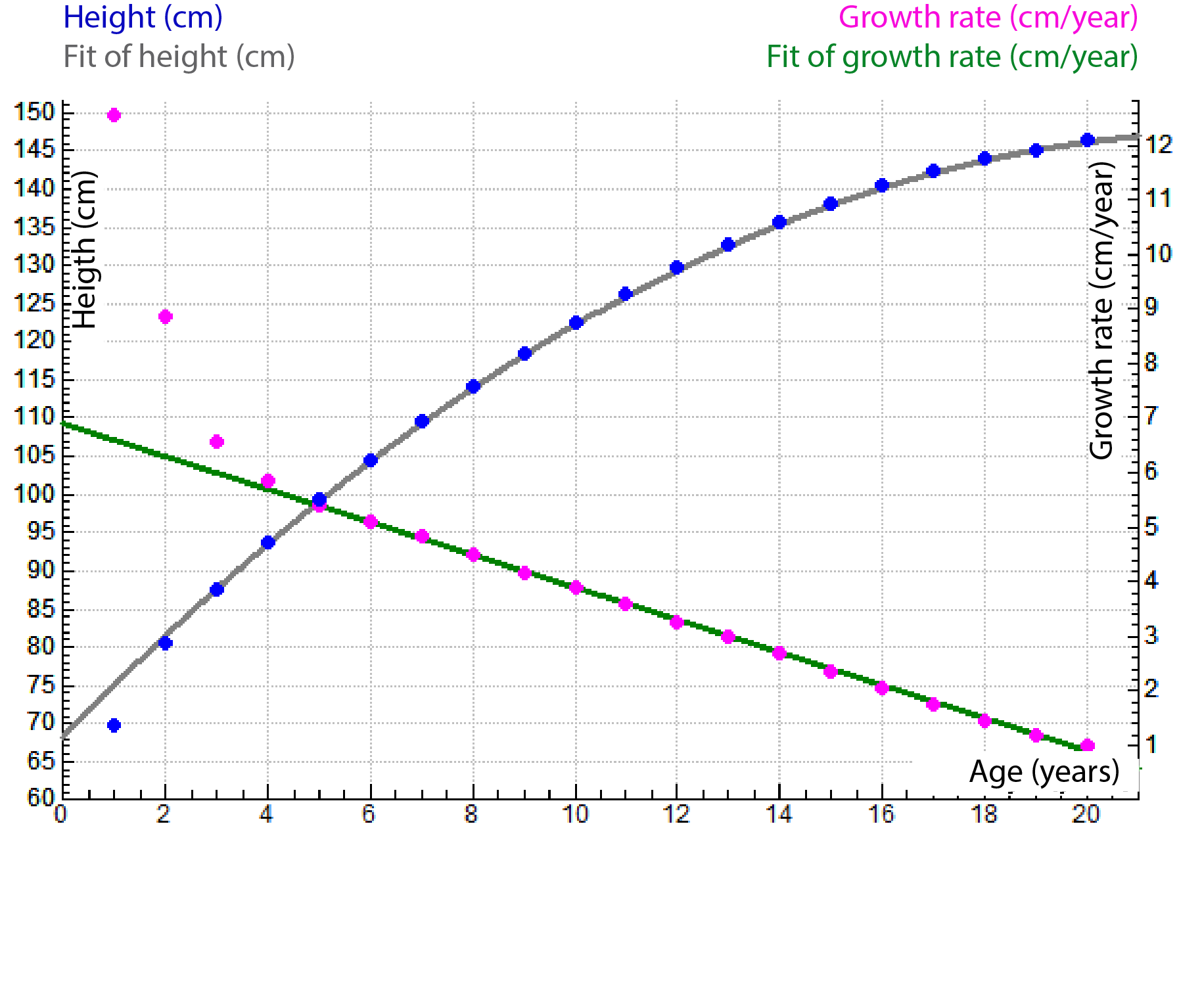
An example of a quadratic relationship is the mathematical modelling of the average height growth of girls with Turner syndrome (a growth disorder caused by chromosomal abnormalities, causing for girls, among other things, retarded height growth and no pubertal growth spurt). The average height \(H(t)\) for age \(t\) greater than five years old appears to be described well by the following quadratic function: \[H(t) = -0.15t^2+6.9t+68.1,\] where length \(H\) is expressed in cm and age \(t\) in years. This formula is found by linear regression to measurements at the age of 5 years of age and later. You can assess the quality of this mathematical model in the diagram below. Here, the average height growth is plotted against age and approximated by the given quadratic function. The growth rate (after the age of 5 years) is also plotted against time (in a second vertical coordinate axis on the right-hand side) and approximated with the straight line given by the linear relationship \[\mathrm{growth\;rate}=6.9-0.30\times\mathrm{age}\tiny.\]