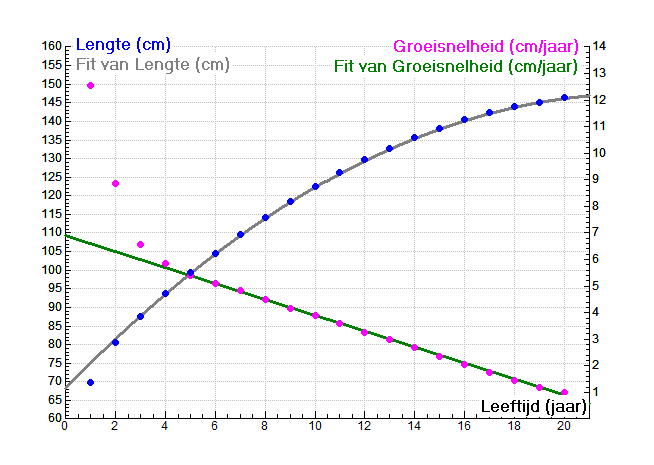
Een voorbeeld van een kwadratisch verband is de wiskundige modellering van de gemiddelde lengtegroei van meisjes met het syndroom van Turner (een groeistoornis veroorzaakt door chromosomale afwijkingen waardoor meisjes o.a. vertraagde lengtegroei en geen puberteitsspurt doormaken). De gemiddelde lengte \(L(t)\) blijkt voor een leeftijd \(t\) groter dan vijf jaar goed te modelleren zijn via de volgende kwadratische functie: \[L(t) = -0.15t^2+6.9t+68.1,\] waarbij lengte \(L\) in cm en leeftijd \(t\) in jaren is uitgedrukt. Deze formule is gevonden door lineaire regressie met de gegeven meting van de leeftijd 5 jaar en later. De kwaliteit van dit wiskundige model voor de beschrijving van de groeigegevens is te beoordelen in onderstaand diagram. Hierin is de gemiddelde lengtegroei uitgezet tegen leeftijd en benaderd met de gegeven kwadratische functie. De groeisnelheid is ook uitgezet tegen de tijd (met een tweede verticale coördinaat-as aan de rechterkant) en na de leeftijd van 5 jaar benaderd met de rechte lijn gegeven door het lineaire verband \[\mathrm{groeisnelheid}=6.9-0.30\times\mathrm{leeftijd}\]