Unlimited growth: Exponential growth
 Introduction
Introduction
In microbiology, you learned that bacteria are single-celled microorganisms, that sometimes live in colonies. You normally cannot see them with the naked eye, but they are omnipresent. Bacteria spoil food and make you sick, but they are also essential for proper digestion, water purification and the production of medicines.
A bacterium is a prokaryote, i.e., a cell without a nucleus. Most prokaryotes reproduce by binary division: a cell grows to approximately double its size and then splits into two genetically identical daughter cells. The simplest model for bacterial growth is, therefore, a discrete model of binary division: after the division of one cell into two daughter cells, the daughter cells divide again and form four cells. Next, a generation of eight cells arises. This may not seem like such a rapid growth of bacteria, but appearances can be deceptive, as the following example illustrates.
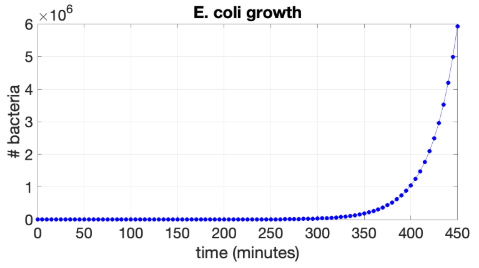
Microbial growth of Escherichia coli (E. coli) bacteria is as follows: every twenty minutes the number of bacteria doubles. Starting from 1 bacterium at the starting time \(t=0\), there are 2 bacteria after 20 minutes, after 40 minutes there are 4 bacteria and after 60 minutes 8 bacteria. The number of bacteria is therefore eight times larger each hour. This might seem like not such a strong growth at a first glance, but look at what happens in the following table:
\[\begin{array}{|l|l|} \hline
\mathit{Time\;} (\mathit{hours}) & \mathit{Number\;of\;bacteria} \\ \hline
0 & 1 \\
1 & 8 \\
2 & 64 \\
3 & 512 \\
4 & 4\,096 \\
5 & 32\,768 \\
6 & 261\,144 \\
7 & 2\,097\,152 \\
8 & 16\,777\,216 \\ \hline \end{array}\]
After roughly 8 hours, 17 million bacteria have emerged by cell division from one bacterium with exponential growth. The number of bacteria for each hour in time \(t\) can be calculated with the formula \(N(t)=8^t\). The graph below illustrates the huge increase in the number of bacteria. We speak of exponential growth.