Limited exponential growth: Introduction
 Why limited growth?
Why limited growth?
Why limited growth? With unlimited growth we studied exponential growth. But the growth continues indefinitely realistic?
The E. Coli bacterium divides into two daughter cells in, say, 20 minutes under optimal conditions.
Question: starting with one bacterium, how many bacteria would follow an exponential growth model after two days?
Answer: in two days, ie 48 hours, there are \(3\times 48=144\) duplications.
The number of bacteria after two days \(2^{144}\approx 2.23\cdot 10^{43}\).
But these numbers do not speak because it is not compared with something recognizable.
So let's estimate the volume.
The diameter of the bacteria is roughly \(10^{-6}\;\mathrm{m}\).
The estimated volume \(2.23\cdot 10^{43}\) bacteria than \(1.17\cdot 10^{25}\,\mathrm{m}^3\).
In comparison, the volume of the Earth is about \(10^{21}\,\mathrm{m}^3\)!
Conclusion: unlimited growth is not realistic in the long run.
Phases in microbial growth A bacterial culture can in theory grow indefinitely, but in practice, it ends because the medium in which the bacteria grow runs out. A commonly used approximation of the exponential growth model for bacterial growth is to separate out the different growth stages:
- the lag phase, in which cells adapt to a new environment before growth can occur;
- the growth phase, in which the growth is exponential and depends only on the combination of intrinsic and extrinsic factors in the growth medium;
- the stationary phase, in which the maximum number of cells has been reached and no further growth takes place;
- the inactivation phase, in which cells are inactivated or killed if conditions are disadvantageous for survival.
When you plot the number of cells against time on logarithmic paper, the graph of limited bacterial growth with the four stages above looks like this:
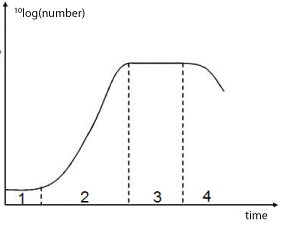
The growth phase is approximately a straight line on a logarithmic scale; the slope of this line is approximately equal to the logarithm of the growth factor \(\bigl(\)so for binary division approximately equal to \(\log_{10}(2)\bigr)\).
This chapter discusses a simple model of limited growth and various applications.


