Limited exponential growth: Limited exponential growth functions
The limited exponential growth function
Definition of the limited exponential growth function The limited exponential growth function is \[y(t)=a-c\cdot e^{-r\cdot t}\] with \(r>0\).
The graph of this function in the case \(c>0\) is outlined below: growth continues to decrease and disappears over time so that the limit \(a\) reached. It is true that \(y(0)=a-c\) and that \(y(t)\) approaches the value \(a\) over time \(t\).
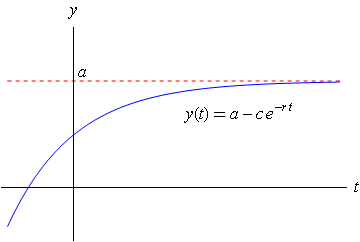
Think about the shape of the graph of \(y(t)\) in case \(c<0\)
Aerobic power \(P_{\mathrm{aer}}\) of a human leg muscle at the start of sprint is mathematically modelled as \[P_{\mathrm{aer}}(t)=P_{\mathrm{max}}\cdot\left(1-e^{-\lambda\cdot t}\right)\] with \(\lambda\approx 0.035\;\mathrm{s}^{-1}\).
The differential equation of the limited exponential growth function \[y(t)=a-c\cdot e^{-r\cdot t}\] with \(r>0\). The derivative of \(y\) is, according to the calculation rules of differentiating, \[y'(t)=c\cdot r\cdot e^{-r\cdot t}\] Because \(c\cdot e^{-r\cdot t}=a-y(t)\) (check!) we know that \[y'(t)=r\cdot\bigl(a-y(t)\bigr)\] This is the differential equation of limited exponential growth, which we will examine in the next theory page.
