Begrensde exponentiële groei: Begrensde exponentiële groeifuncties
De begrensde exponentiële groeifunctie
Definitie van de begrensde exponentiële groeifunctie De begrensde exponentiële groeifunctie is \[y(t)=a-c\cdot e^{-r\cdot t}\] met \(r>0\).
De grafiek van deze functie in het geval \(c>0\) is hieronder geschetst: de groei neemt steeds verder af en verdwijnt op den duur zodat de functie de grenswaarde \(a\) bereikt. Er geldt dat \(y(0)=a-c\) en dat \(y(t)\) de waarde \(a\) meer nadert naarmate de tijd \(t\) verstrijkt.
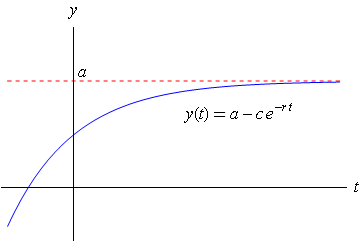
Bedenk zelf hoe de grafiek van \(y(t)\) verloopt in het geval \(c<0\).
Het aerobe vermogen \(P_{\mathrm{aer}}\) van spieren bij het begin van een inspanning wordt wiskundig gemodelleerd als \[P_{\mathrm{aer}}(t)=P_{\mathrm{max}}\cdot\left(1-e^{-\lambda\cdot t}\right)\] met \(\lambda\approx 0.035\;\mathrm{s}^{-1}\).
Differentiaalvergelijking van begrensde exponentiële functie \[y(t)=a-c\cdot e^{-r\cdot t}\] met \(r>0\). De afgeleide van \(y\) is dan volgens de rekenregels van differentiëren \[y'(t)=c\cdot r\cdot e^{-r\cdot t}\] Omdat \(c\cdot e^{-r\cdot t}=a-y(t)\) (ga na!) geldt \[y'(t)=r\cdot\bigl(a-y(t)\bigr)\] Dit is de differentiaalvergelijking van begrensde exponentiële groei, die we in de volgende theoriepagina onder de loep zullen nemen.
