Begrensde exponentiële groei: Toepassingen
 Reactiekinetiek van een unimoleculaire evenwichtsreactie
Reactiekinetiek van een unimoleculaire evenwichtsreactie
voorwaarts \(\displaystyle \text{A}\stackrel{k_1}{\longrightarrow} \text{B}\) met reactiesnelheidsconstante \(k_1\)
terugwaarts \(\displaystyle \text{B}\stackrel{k_{2}}{\longrightarrow} \text{A}\) met reactiesnelheidsconstante \(k_{2}\)
Stof A verdwijnt niet alleen, maar wordt ook gevormd uit stof B door de terugwaartse reactie. Evenzo wordt stof B niet alleen gevormd, maar verdwijnt het ook weer door de terugwaartse reactie. Als we uitgaan van elementaire chemische reacties in dit systeem, dan beschrijven de volgende twee gekoppelde differentiaalvergelijkingen de reactiekinetiek: \[\left\{\begin{aligned}\frac{\dd[\text{A}]}{\dd t}&=-k_1[\text{A}]+k_{2}[\text{B}]\\ \\ \frac{\dd[\text{B}]}{\dd t}&=k_1[\text{A}]-k_{2} [\text{B}]\end{aligned}\right.\] Onder de veronderstelling dat de totale concentratie van A en B constant is, kun je de differentiaalvergelijkingen ontkoppelen: als \([\text{A}]+[\text{B}]=K\) voor zekere constante \(K\), dan kun je de differentiaalvergelijkingen herschrijven als \[\begin{aligned}\frac{\dd[\text{A}]}{\dd t}&=-k_1 [\text{A}]+k_{2} (K-[\text{A}])\\ \\ \frac{\dd[\text{B}]}{\dd t}&=k_1 (K-[\text{B}])-k_{2}[\text{B}]\end{aligned}\] oftewel als \[\begin{aligned}\frac{\dd[\text{A}]}{\dd t}&=k_{2} K-(k_1+k_{2}) [\text{A}]\\ \\ \frac{\dd[\text{B}]}{\dd t}&=k_1 K-(k_1+k_{2}) [\text{B}]\end{aligned}\] Beide differentiaalvergelijkingen horen bij begrensde exponentiële groei en na voldoende tijd stelt het evenwicht zich in.
Er is sprake van chemisch evenwicht als \[\frac{\dd[\text{A}]}{\dd t}=0, \frac{\dd[\text{B}]}{\dd t}=0\] De evenwichtsconcentraties \([\text{A}]_{\infty}\) en \([\text{B}]_{\infty}\) zijn hiermee uit te rekenen; ga na dat in evenwicht geldt \[[\text{A}]_{\infty}=\frac{k_{-1}\cdot c}{(k_1+k_{-1})},\quad [\text{B}]_{\infty}=\frac{k_{1}\cdot c}{(k_1+k_{-1})}\] In evenwicht verhouden de concentraties zich als quotiënt van de voorwaartse en terugwaartse reactiesnelheidsconstanten: \[\frac{[\text{A}]_{\infty}}{[\text{B}]_{\infty}} = \frac{k_{-1}}{k_{1}}\]
Als concreet voorbeeld bekijken we de reactiekinetiek van de isomerisatie
\[\mathit{cis\mbox{-}}\mathrm{Mo(CO)}_4 \mathrm{[P(}\mathit{n}\,\mbox{-}\mathrm{Bu)}_3\mathrm{]}_2\rightleftharpoons \mathit{trans\mbox{-}}\mathrm{Mo(CO)}_4 \mathrm{[P(}\mathit{n}\,\mbox{-}\mathrm{Bu)}_3\mathrm{]}_2\] De reactiesnelheidsconstanten (in \(\mathrm{s}^{-1}\)) zijn afhankelijk van de temperatuur \(T\) (in Kelvin) volgens de volgende formules (Bengali & Mooney, 2003): \[k_1=T\cdot 10^{8.87-\frac{5195}{T}},\quad k_{-1}=T\cdot 10^{8.78-\frac{5394}{T}}\] Onderstaand diagram laat het verloop van de concentraties van de cis- en trans-vorm (in μM) zien bij een temperatuur van \(85{}^{\circ}\!\mathrm{C}\). Beide krommen passen bij begrensde exponentiële groei.
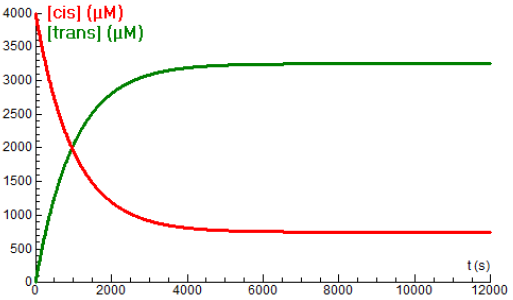
Hieronder staan de concentratiekrommen bij een temperatuur van \(80{}^{\circ}\!\mathrm{C}\). De eerdere krommen passend bij \(85{}^{\circ}\!\mathrm{C}\) zijn grijsgetint.
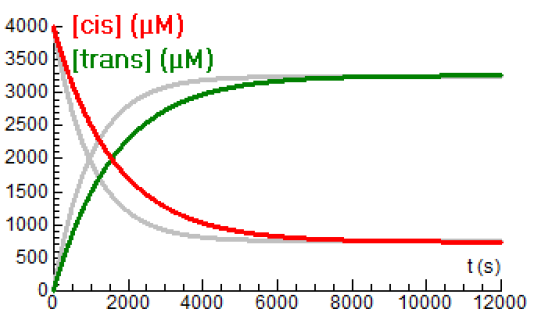
Je ziet in het diagram dat de evenwichtsconcentraties nauwelijks verschillen, maar dat het ene evenwicht trager bereikt wordt dan het andere evenwicht. Klaarblijkelijk blijft de ratio van de reactiesnelheidsconstanten nagenoeg gelijk.
Bengali, A.A. & Mooney, K.E. (2003). Synthesis, kinetics, and thermodynamics: an advanced laboratory investigation of the cis-trans isomerization of \(\mathrm{Mo(CO)}_4\mathrm{(PR}_3\mathrm{)}_2.\) Journal of Chemical Education 80(9), 1044-1047.


