Differentiaalvergelijking van begrensde exponentiële groei

Begrensde exponentiële groei: Begrensde exponentiële groeifuncties

Differentiaalvergelijking van begrensde exponentiële groei

In de inleiding zijn we de differentiaalvergelijking van begrensde exponentiële groei al tegen gekomen en hebben we de differentiaalvergelijking opgelost in twee verschillende contexten.

De algemene oplossing van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=r\cdot(a-y)\] met constanten \(a>0,\;r>0\) is \[y(t)=a-c\cdot e^{-r\cdot t}\] voor zekere constante \(c\).

Voor de liefhebber bewijzen we dat de algemene oplossing van de differentiaalvergelijking \[\frac{dy}{dt}=r\cdot(a-y)\] met constanten \(a>0,\;r>0\) gelijk is \[y(t)=a-c\cdot e^{-r\cdot t}\] voor zekere constante \(c\).

Begin met een nieuwe grootheid \(z(t)\) te introduceren via \[z=y-a\] Dan geldt \[\begin{aligned}\frac{\dd z}{\dd t}&=\frac{\dd(y-a)}{\dd t}\\ \\ &=\frac{\dd y}{\dd t}\\[0.25cm] &= r\cdot(a-y)\\[0.25cm] &= -r\cdot z\end{aligned}\] De grootheid \(z\) voldoet dus aan de differentiaalvergelijking van exponentieel verval, \(z'(t)=-r\cdot z(t)\), en de algemene oplossing kan geschreven worden als \[z(t)=-c\cdot e^{-r\cdot t}\] voor zekere constante \(c\). Maar dan geldt dus \[y(t)=a+z(t)=a-c \cdot e^{-r\cdot t}\]

Overigens kun je de differentiaalvergelijking ook op een andere manier oplossen. Uit \[\frac{\dd y}{\dd t}=r\cdot(a-y)\] volgt \[\frac{\displaystyle\frac{\dd y}{\dd t}}{a-y}=r\] Nu denk je wellicht dat je niks opgeschoten bent, maar de linkerkant is de afgeleide van een bekende uitdrukking; met de kettingregel volgt de volgende herschrijving \[\frac{\dd(-\ln\bigl(|a-y|\bigr)}{\dd t}=r\] oftewel de afgeleide van \(\ln\bigl(|a-y|\bigr)\) moet gelijk zijn aan \(-r\). Maar dan verschillen de functies \(\ln\bigl(|a-y|\bigr)\) en \(-r\cdot t\) slechts een constante, zeg \(c\): \[\ln\bigl(|a-y|\bigr)=-r\cdot t + c\] oftewel \[|a-y| = e^{-r\cdot t+c}\] Maar dan \[y=a-C \cdot e^{-r\cdot t}\] met \(C=\pm e^c\).

Geef de oplossing van de differentiaalvergelijking \[\frac{dy}{dt}=0.10\cdot(25-y)\] met \(y=14\) wanneer \(t=4\).

De differentiaalvergelijking hoort bij geremde exponentiële groei en de algemene oplossing is dus \[y(t)=25-c\cdot e^{-0.10t}\] Omdat \(y(4)=14\) kunnen we een vergelijking voor \(c\) opstellen: \[14=25-c\cdot e^{-0.10\cdot 4}\] oftewel \[c\cdot e^{-0.4}=25-14=11\] Maar dan geldt \[c=11\cdot e^{0.4}\approx 16.41\]

Nieuw voorbeeld

Aymptotiek en stabiliteit Ook al kunnen we deze differentiaalvergelijking oplossen in expliciete vorm, toch is het interessant om te kijken naar hoe uit de differentiaalvergelijking zelf al veel informatie over de mogelijke oplossingen te halen valt.

Als je bijvoorbeeld wilt weten of en welke evenwichtsoplossingen er zijn in het dynamisch model, dan kun je daar achter komen door de vergelijking \(\frac{\dd y}{\dd t}=0\) op te lossen: omdat de afgeleide gelijk aan 0 is, verandert de grootheid \(y\) dan niet meer. We spreken van een evenwicht. In dit geval is \(y(t)=a\) de enige evenwichtsoplossing. Als de grootheid \(y\) op een zeker tijdstip een waarde aanneemt kleiner dan \(a\), dan is de afgeleide daar groter dan nul en stijgt de oplossingskromme op dat moment. Als de grootheid \(y\) op een zeker tijdstip een waarde aanneemt kleiner dan \(a\), dan is de afgeleide daar kleiner dan nul en daalt de oplossingskromme op dat moment. Bij kleine uitwijkingen van het evenwicht keer je dus van lieverlee weer terug naar het evenwicht. We zeggen dat het evenwicht aantrekkend is.

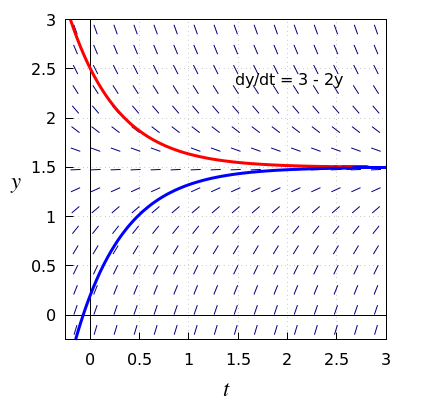
Gedrag van oplossingen ten toon gespreid in een lijnelementenveld Om te weten hoe oplossingen van de differentiaalvergelijking zich in de buurt van deze evenwichtsoplossing gedragen, kun je ook het lijnelementenveld bestuderen.

Als concreet voorbeeld is hieronder het lijnelementenveld van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=3-2y\] getekend samen met twee oplossingskrommen. De krommen ontstaan door de lijntjes in het lijnelementenveld in kleine stapjes te volgen. Er is hier sprake van een aantrekkend evenwicht: elke oplossing in de buurt van de evenwichtsoplossing nadert de evenwichtsoplossing; sterker nog in dit voorbeeld nadert elke oplossing na verloop van tijd de evenwichtsoplossing. Zonder de oplossing expliciet te kennen, is het met het lijnelementenveld al mogelijk om in te zien wat het gedrag van oplossingen zal zijn.

lijnelementenveld van de begrensde exponentiële groeifunctie

Interactieve versie van een lijnelementenveld Voor wie het model beter wil leren begrijpen via het lijnelementenveld: Je kunt spelen met onderstaande interactieve versie van het lijnelementenveld bij een differentiaalvergelijking. Als voorbeeld is bovenstaande differentiaalvergelijking van begrensde exponentiële groei klaargezet met een exponentiële kromme als voorbeeld van één van de vele mogelijke oplossingskrommen, maar je kunt de wiskundige formule aanpassen. Door het punt \(P\) te verslepen zie je verschillende oplossingskrommen. Je kunt instellingen wijzigen en dan met de update knop de nieuwe situatie in beeld krijgen.