Definitie en basiseigenschappen

Logistische groei: De logistische functie

Definitie en basiseigenschappen

De logistische functie, ook wel sigmoïdefunctie genoemd, is \[y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\] met \(a>0\) en \(c>0\). De grafiek van deze functie in het geval \(r>0\) is hieronder geschetst: de grafiek is een stijgende sigmoïde, d.w.z. het een s-vorm doordat de groei eerst steeds verder toeneemt, en later steeds verder afneemt en op den duur verdwijnt zodat de functie de grenswaarde \(a\) bereikt. Er geldt dat \(y(0)=\frac{a}{1+c}\) en dat \(y(t)\) de waarde \(a\) meer nadert naarmate de tijd \(t\) verstrijkt. De parameter \(a\) heet in het logistische groeimodel de draagkracht en \(r\) heet de intrinsieke groeicoëfficiënt.

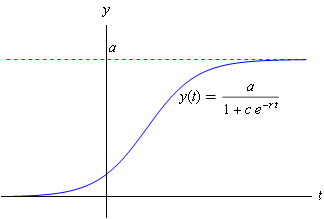
grafiek van de logistische groeifunctie

Bedenk zelf hoe de grafiek van \(y(t)\) verloopt in het geval \(r<0\).

Een speciaal geval is de logistische functie \[\sigma(x)=\frac{1}{1+e^{-x}}\] Deze functie beeldt reële waarden af op het interval \((0,1)\) en wordt in neurale netwerktheorie veel gebruikt om responswaarden te begrenzen.

De afgeleide van de logistische functie \(\displaystyle y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\) is volgens de rekenregels van differentiëren te berekenen en voldoet aan de relatie \[\frac{\dd y}{\dd t}=\frac{r}{a}\cdot y\cdot (a-y)\] Dit is de differentiaalvergelijking voor logistische groei.
Soms wordt deze ook geschreven als \[\frac{\dd y}{\dd t}=r\cdot y\cdot \bigl(1-\frac{y}{a}\bigr)\] We spreken van het logistische groeimodel, ook bekend als het Verhulst model.

Voor de liefhebber bewijzen we dat de afgeleide van de logistische functie \(\displaystyle y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\) voldoet aan de relatie \[\frac{\dd y}{\dd t}=\frac{r}{a}\cdot y\cdot (a-y)\]

Met de rekenregels voor differentiëren is de afgeleide \(y'(t)\) uit te rekenen: \[\begin{aligned}y(t)&=\frac{a}{1+c\cdot e^{-r\cdot t}}\\ \\ &=a\cdot\left(1+c\cdot e^{-r\cdot t}\right)^{-1}\end{aligned}\] en de afgeleide is dus \[\begin{aligned}y'(t)&=-a\cdot\left(1+c\cdot e^{-r\cdot t}\right)^{-2}\cdot \left(c\cdot r\cdot e^{-r\cdot t}\right)\\ \\ &=\frac{a}{1+c\cdot e^{-r\cdot t}}\cdot \frac{c\cdot r\cdot e^{-r\cdot t}}{1+c\cdot e^{-r\cdot t}}\\ \\ &= \frac{a}{1+c\cdot e^{-r\cdot t}}\cdot \frac{r}{a}\cdot \frac{a\cdot c\cdot e^{-r\cdot t}}{1+c\cdot e^{-r\cdot t}}\end{aligned}\] omdat \[\begin{aligned}a-y(t)&=a-\frac{a}{1+c\cdot e^{-r\cdot t}}\\ \\ &=\frac{a\cdot c\cdot e^{-r\cdot t}}{1+c\cdot e^{-r\cdot t}}\end{aligned}\] geldt dus \[y'(t)=\frac{r}{a}\cdot y(t)\cdot \bigl(a-y(t)\bigr)\]

De algemene oplossing van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=r\cdot y\cdot \bigl(1-\frac{y}{a}\bigr)\] met constanten \(a>0\) en \(r\) is gelijk aan \[y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\] voor zekere constante \(c\).

De constante \(c\) wordt vaak bepaald door de beginwaarde \(y(0)\). Alleen in het geval van \(c>0\), d.w.z. als \(y(0)\) tussen 0 en \(a\) in ligt, is er sprake van een logistische functie met een sigmoïde als grafiek.

Voor de liefhebber geven we een bewijs waarin de slimme truc bestaat uit de introductie van een nieuwe grootheid \(z(t)\) via de relatie \(y=\frac{1}{z}\). Dan blijkt \(z\) te voldoen aan de differentiaalvergelijking van begrensde exponentiële groei, waarvan we de oplossing al kennen. Er geldt namelijk

\[\begin{aligned} \frac{\dd\left(\frac{1}{z}\right)}{\dd t} &= r\cdot\left(\frac{1}{z}\right)\cdot\left(1-\frac{\frac{1}{z}}{a}\right)\\ \\ -\frac{1}{z^2}\frac{dz}{dt}&=r\cdot\frac{1}{z}\left(1-\frac{1}{a\cdot z}\right)\\ \\ \frac{\dd z}{\dd t} &= r\cdot\left(\frac{1}{a}-z\right)\quad (\text{na vermenigvuldiging met }-z^2). \end{aligned}\] De grootheid \(z\) voldoet dus aan de differentiaalvergelijking van geremde exponentiële groei en de algemene oplossing kan geschreven worden als \[\begin{aligned}z(t) &=\frac{1}{a}+C\cdot e^{-r\cdot t}\\ \\ &= \frac{1+c\cdot e^{-r\cdot t}}{a}\end{aligned}\] met \(c=a\, C\) voor zekere constante \(C\). We hebben dus gevonden \[y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\] voor zekere constante \(c\).

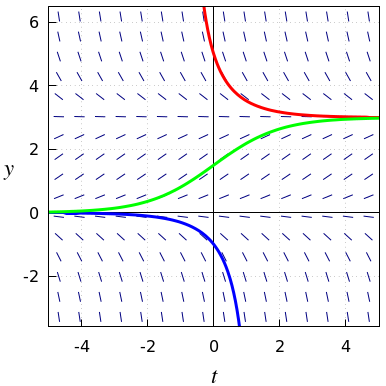
Een concreet voorbeeld van een logistische differentiaalvergelijking is \[\frac{\dd y}{\dd t}=y\cdot \left(1-\frac{y}{3}\right)\] In onderstaand lijnelementenveld zijn drie oplossingskrommen getekend. Je krijgt dergelijke krommen door de de lijntjes in het lijnelementenveld in kleine stapjes te volgen. Zo hoort de groen getekende s-vormige kromme bij de oplossing \(\displaystyle y(t)=\frac{3}{1+e^{-t}}\) met beginwaarde \(y(0)=1\!\tfrac{1}{2}\). De twee andere krommen, horende bij beginwaarden \(y(0)\) buiten het interval \([0,a]\), hebben niet de vorm van een sigmoïde. Wat het diagram ook illustreert is dat in dit voorbeeld de evenwichtstoestand \(y=3\) aantrekkend is: elke oplossingskromme die eenmaal in de buurt van deze rechte lijn loopt nadert bij toenemende tijd dit evenwicht. Bij de evenwichtstoestand \(y=0\) is het juist andersom: dit evenwicht is afstotend, d.w.z elke oplossingskromme die er op zeker moment een klein beetje van afwijkt zal steeds verder weglopen van dit evenwicht.

logistische groei

Interactieve versie van een lijnelementenveld Voor wie het model beter wil leren begrijpen via het lijnelementenveld: Je kunt spelen met onderstaande interactieve versie van het lijnelementenveld bij een differentiaalvergelijking. Als voorbeeld is bovenstaande differentiaalvergelijking van begrensde exponentiële groei klaargezet met een exponentiële kromme als voorbeeld van één van de vele mogelijke oplossingskrommen, maar je kunt de wiskundige formule aanpassen. Door het rode punt op de kromme te verslepen zie je verschillende oplossingskrommen. Dit interactieve diagram bevat ook een verplaatsbare 'cursor' die op elke positie een bijpassend lijnelement laat zien

GeoGebra

Los de differentiaalvergelijking \[\frac{\dd y}{\dd t}=0.6\cdot y\cdot (1-0.01y)\] op in expliciete vorm als de beginwaarde \(y(0)=11\) is.

De differentiaalvergelijking is \[\frac{\dd y}{\dd t}=0.6\cdot y\cdot \bigl(1-0.01\cdot y\bigr)=0.6\cdot y\cdot \bigl(1-\frac{y}{100}\bigr)\] We hebben dus te maken met een speciaal geval van de logistische vergelijking \[\frac{\dd y}{\dd t}=r\cdot y\cdot \left(1-\frac{y}{a}\right)\] met \[r=0.6,\;a=100\] De oplossing van de algemene logistische vergelijking is \[y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\] voor zekere constante \(c\). In dit geval hebben we dus een oplossing \[y(t)=\frac{100}{1+c\cdot e^{-0.6\cdot t}}\] De constante \(c\) berekenen we door de vergelijking \(y(0)=11\) op te lossen.
Omdat \(e^0=1\) moeten we de vergelijking \[y(t)=\frac{100}{1+c}=11\] oplossen. Dit kan als volgt: \[\begin{aligned}\frac{100}{1+c}=11 &\stackrel{\blue{\times(1+c)}}{\implies} 100=11\cdot(1+c)\\ \\ &\stackrel{\blue{\mathrm{haakjes}}}{\implies} 100=11+11c\\ \\ &\stackrel{\blue{-11}}{\implies} 100-11=11c\\ \\ &\stackrel{\blue{\div 11}}{\implies} c=\frac{100-11}{11}={{89}\over{11}}\approx 8.09\end{aligned}\] De grafiek van \(y(t)\) is

Nieuw voorbeeld