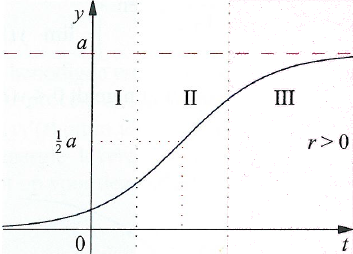
Phase I If $y$ is very small, then $1-\frac{y}{a}$ is approximately equal to $1$.
So, in this stage $y'(t)\approx r\cdot y$.

In other words, in the early stages of growth there is growth that is very similar to exponential growth with growth rate $r$.

Phase II In this phase, the growth rate reaches a maximum value at the moment when $y=\tfrac{1}{2}a$. We can calculate the time at which this happens: you just need to solve $y(t)=\tfrac{1}{2}a$ for $t$. This can be done as follows:

$$\begin{aligned} y(t)=\tfrac{1}{2}a &\implies \frac{a}{1+c\cdot e^{-r\cdot t}}=\frac{a}{2}\\ \\ &\implies 1+c\cdot e^{-r\cdot t}=2\\ \\ &\implies c\cdot e^{-r\cdot t}=1\\ \\ &\implies c=e^{r\cdot t}\\ \\ &\implies \ln(c)= r\cdot t\\ \\ &\implies t=\frac{\ln(c)}{r}\end{aligned}$$ Parameter $c$ can be expressed in the initial value $y(0)=y_0$: $$c=\frac{a}{y_0}-1$$ Check that this formula for $c$ is correct. This is a simple expression in the relative initial value $\displaystyle\frac{y_0}{a}$.

From the derivation above it follows that the time at which the growth rate reaches a maximum is

$$t = \frac{\ln(\frac{a}{y_0}-1)}{r}$$ which depends on the ratio between the initial value $y_0$ and the maximum value $a$, the so-called relative initial value. So basically, the moment of maximal growth does not depend on the maximum value or initial value per se, but only on what ratio, or on what percentage, of the maximum value the growth starts (and on the growth rate). So if you start at 20% of the maximum value, the maximum growth will always occur at $t = \frac{\ln (4)}{r}$, independent of the maximum value.

Phase III When $y(t)$ is very close to the value $a$, then $r\cdot y\approx r\cdot a$, and therefore $y'(t)\approx r\cdot \bigl(a-y(t)\bigr)=r\cdot a-r\cdot y.$

Thus, in the final stage we are dealing with growth that resembles limited exponential growth.