Logistische groei: De logistische functie
 Gedrag van de logistische functie
Gedrag van de logistische functie
We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=r\cdot y\cdot \left(1-\frac{y}{a}\right)\] met parameters \(r>0\) en \(a>0\), en we vragen ons af wat er over het gedrag van de oplossingen met een beginwaarde \(y(0)\) tussen \(0\) en \(a\) te zeggen valt.
De afgeleide \(\displaystyle\frac{\dd y}{\dd t}\) is te beschouwen als een functie van \(y\) met als grafiek een bergparabool met nulpunten \(y=0\) en \(y=a\). Deze functie heeft een maximum halverwege tussen de nulpunten, d.w.z. in \(y=\tfrac{1}{2}\!a\). De maximale groeisnelheid is dan \(\tfrac{1}{4}r\cdot a\).
De grafiek van de stijgende logistische functie \[y(t)=\frac{a}{1+c\cdot e^{-r\cdot t}}\] die de algemene oplossing is van de logistische differentiaalvergelijking \[\frac{\dd y}{\dd t}=r\cdot y\cdot \left(1-\frac{y}{a}\right)\] met \(r>0,\;a>0\) kan in drie fasen onderverdeeld worden. Zie onderstaande figuur.
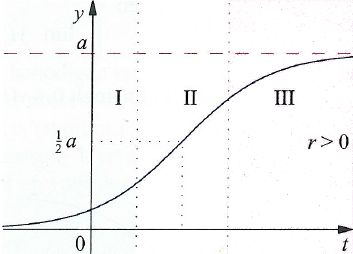
Fase I Als \(y\) erg klein is, dan is \(1-\frac{y}{a}\) ongeveer gelijk aan \(1\).
Dus in deze fase geldt \(y'(t)\approx r\cdot y\).
Met andere woorden, er is in de beginfase sprake van groei die erg lijkt op exponentiële groei met relatieve groeisnelheidsconstante \(r\).
Fase II In deze fase bereikt de groeisnelheid een maximale waarde op het moment dat \(y=\tfrac{1}{2}a\). Het tijdstip waarop dit gebeurt is ook uit te rekenen: je hoeft alleen maar de vergelijking \(y(t)=\tfrac{1}{2}a\) in \(t\) op te lossen. Dit kan als volgt: \[\begin{aligned} y(t)=\tfrac{1}{2}a &\implies \frac{a}{1+c\cdot e^{-r\cdot t}}=\frac{a}{2}\\ \\ &\implies 1+c\cdot e^{-r\cdot t}=2\\ \\ &\implies c\cdot e^{-r\cdot t}=1\\ \\ &\implies c=e^{r\cdot t}\\ \\ &\implies \ln(c)= r\cdot t\\ \\ &\implies t=\frac{\ln(c)}{r}\end{aligned}\] De parameter \(c\) kun je uitdrukken in de beginwaarde \(y(0)=y_0\):\[c=\frac{a}{y_0}-1\] Ga zelf na dat de formule voor \(c\) klopt. Dit is een eenvoudige uitdrukking in de relatieve beginwaarde \(\displaystyle\frac{y_0}{a}\).
Uit het voorafgaande volgt dus dat het tijdstip waarop de maximale groeisnelheid bereikt wordt enkel en alleen van de intrinsieke groeisnelheid en relatieve beginwaarde afhangt.
Fase III Als \(y(t)\) heel dicht bij de waarde \(a\) is, dan geldt dat de grootheid \(r\cdot y\approx r\cdot a\) en dus \(y'(t)\approx r\cdot \bigl(a-y(t)\bigr)=r\cdot a-r\cdot y.\)
We hebben in de eindfase dus te maken met groei die sterk lijkt op begrensde exponentiële groei.


