Functions and graphs: Function machines and composition of functions
 Combining functions
Combining functions
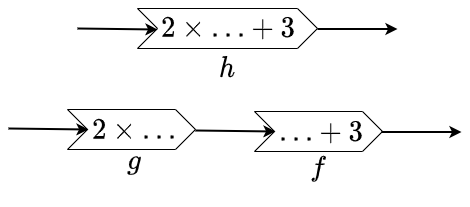
Below is a function machine, named \(h\), with a verbal function definition "double the input and add two" and with the mathematical formula \(h(x)=2x+3\). Below this function machine is a chain of two function machines, named \(g\) and \(f\), which belong to the function definitions "double the input" and "add two to the input" and thus to the formulas \(g(x)=2x\) and \(f(x)=x+3\). The chain indicates that one must first use machine \(g\) and hereafter the function machine \(f\). The result is the same as the one after applying function machine \(h\). In other words, machines \(g\) and \(f\) are building blocks for the machine \(h\). We denote this chaining as \(f\circ g\) and call it the composition of the functies \(f\) and \(g\). In this example \(h=f\circ g\), i.e., \(h(x)=f(g(x))\) for an arbitrary argument \(x\).
The standard functions are the building blocks to create new functions. They are full mathematical objects that can be added, multiplied and divided. You can also apply function in succession. The result is then a composite function.
The sum function, difference function, product function, quotient function and composite function construct from two known functions \(f\) and \(g\) are defined as follows:
\[\begin{aligned}
(f+g)(x) &= f(x)+g(x) \\ \\
(f-g)(x) &= f(x)-g(x) \\ \\
(f\cdot g)(x) &= f(x)\cdot g(x)\\ \\
\left(\frac{f}{g}\right)(x) &= \frac{f(x)}{g(x)} \\ \\
(f\circ g)(x) &= f(g(x))
\end{aligned}\]
An illustrative example of composition of two functions is the definition of the function \(h(x)=\sin(x^2)+1\).
You can consider \(h\) as the composition of the function \(f(u)=\sin(u)+1\) and the function \(g(x)=x^2\).
After all: \((f\circ g)(x) = f(g(x))= f(x^2)=\sin(x^2)+1\).
You can consider the composite function as a chain of functions:
The function \(h(x)=\sin(x^2)+1\) can be split into \(y=\sin(u)+1\) with \(u=x^2\).
Indeed, substitution of \(u=x^2\) in \(y=\sin(u)+1\) results again in the function \(h(x)=\sin(x^2) +1\).
Also note that the function \(f\circ g\) is not the same as \(g\circ f\). After all, \((g\circ f)(x)=g(f(x))=(\sin(x)+1)^2\).
Iteration of a function If \(f\) is a function with equal domain and range, then the composition \(f\circ f\) is also written as \(f^2\) and further recursively \(f^n=f^{n-1}\circ f\) for \(n=3,4,\ldots\) We call this iteration of the function. This notation is a bit confusing without the annotation "iteration" because this notation is also commonly used for a repeated product of functions.
Inverse function
Two functions \(f\) and \(g\) are each other's inverse if \(f\circ g\) and \(g\circ f\) are equal to the identity mapping. The inverse function of\(f\) we denote as \(f^{\mathrm{inv}}\) or as \(f^{-1}\). Nor every function has an inverse. When a function does have an inverse then we speak about an invertible function.
Some examples of invertible functions: \[\begin{aligned}f(x)&=\phantom{2}x+1\text{ has as inverse function }f^{-1}(x)=x-1\\[0.25cm] g(x)&=2x\phantom{+1}\text{ has as inverse function }g^{-1}(x)=\tfrac{1}{2}x\\[0.25cm] h(x)&=2x+3\text{ has as inverse function }h^{-1}(x)=\tfrac{1}{2}(x-3)\end{aligned}\] The graph of \(f^{-1}\) can be obtained from the graph of \(f\) by exchanging the \(x\) and \(y\) coordinates of all points of the graph of\(f\). The graphs are each other's mirror image with respect to reflection in the line \(y=x\).
Mathcentre videos
Composition of Functions (10:51)
#\phantom{x}#
Inverse Functions (17:57)


