Functies en grafieken: Functiemachientjes en samenstelling van functies
 Functies combineren
Functies combineren
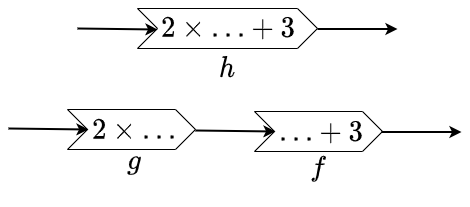
Hieronder zie je een functiemachientje, \(h\) genaamd, met als functievoorschrift in woorden "verdubbel de invoer en tel er daarna twee bij op" en in formulevorm \(h(x)=2x+3\). Onder dit functiemachientje staat een keten van twee functiemachientjes, \(g\) en \(f\) genaamd, die horen bij de functievoorschriften "verdubbel de invoer" en "tel twee op bij de invoer" en dus bij de formulevormen \(g(x)=2x\) en \(f(x)=x+3\). De keten geeft aan dat je eerst machientje \(g\) moet gebruiken en vervolgens het machientje \(f\). Het resultaat is hetzelfde als toepassen van het functiemachientje \(h\). Anders gezegd, fungeren de machientje \(g\) en \(f\) als bouwstenen voor het machientje \(h\). We noteren dit bouwwerk als \(f\circ g\) en spreken van een samenstelling van de functies \(f\) en \(g\). Er geldt hier dus dat \(h=f\circ g\), dat wil zeggen \(h(x)=f(g(x))\) voor een willekeurig argument \(x\).
Standaardfuncties fungeren ook als bouwstenen om nieuwe functies te maken. Het zijn volwaardige wiskundige objecten waarmee je kan optellen, vermenigvuldigen en delen. Je kan ze optellen en met elkaar vermenigvuldigen, maar ook achter elkaar toepassen. Het resultaat is dan een geschakelde functie, beter bekend onder de naam samengestelde functie.
De somfunctie, verschilfunctie, productfunctie, quotiëntfunctie en samengestelde functie opgebouwd uit twee bekende functies \(f\) en \(g\) worden als volgt gedefinieerd:
\[\begin{aligned}
(f+g)(x) &= f(x)+g(x) \\ \\
(f-g)(x) &= f(x)-g(x) \\ \\
(f\cdot g)(x) &= f(x)\cdot g(x)\\ \\
\left(\frac{f}{g}\right)(x) &= \frac{f(x)}{g(x)} \\ \\
(f\circ g)(x) &= f\bigl(g(x)\bigr)
\end{aligned}\]
Een voorbeeld ter illustratie van samenstelling van twee standaardfuncties is de definitie van de functie \(h(x)=\sin(x^2)+1\).
Je kan \(h\) beschouwen als de samenstelling van de functie \(f(u)=\sin(u)+1\) en de functie \(g(x)=x^2\).
Immers: \((f\circ g)(x) = f(g(x))= f(x^2)=\sin(x^2)+1\).
Je kunt de samengestelde functie zien als een schakel van functies:
de functie \(h(x)=\sin(x^2)+1\) kun je opsplitsen in \(y=\sin(u)+1\) met \(u=x^2\).
Inderdaad geeft substitutie van \(u=x^2\) in \(y=\sin(u)+1\) weer de functie \(h(x)=\sin(x^2) +1\).
Merk ook op de functie \(f\circ g\) niet gelijk is aan \(g\circ f\). Immers, \((g\circ f)(x)=g(f(x))=(\sin(x)+1)^2\).
Iteratie van een functie Als \(f\) een functie is met gelijk domein en beeld, dan wordt de samenstelling \(f\circ f\) soms ook wel geschreven als \(f^2\) en verder recursief \(f^n=f^{n-1}\circ f\) voor \(n=3,4,\ldots\) We spreken dat van iteratie van de functie. Deze notatie is verwarrend zonder de toevoeging iteratie omdat de notatie ook voor een herhaald product van functies gangbaar is.
Inverse functie
Twee functies \(f\) en \(g\) zijn elkaars inverse als \(f\circ g\) en \(g\circ f\) gelijk zijn aan de identieke afbeelding. De inverse functie van \(f\) noteren we als \(f^{\mathrm{inv}}\) of als \(f^{-1}\). Niet elke functie heeft een inverse. Als een functie wel een inverse heeft dan spreken we van een inverteerbare functie.
Enkele voorbeelden van inverteerbare functies: \[\begin{aligned}f(x)&=\phantom{2}x+1\text{ heeft als inverse functie }f^{-1}(x)=x-1\\[0.25cm] g(x)&=2x\phantom{+1}\text{ heeft als inverse functie }g^{-1}(x)=\tfrac{1}{2}x\\[0.25cm] h(x)&=2x+3\text{ heeft als inverse functie }h^{-1}(x)=\tfrac{1}{2}(x-3)\end{aligned}\] Je krijgt de grafiek van \(f^{-1}\) krijg je door bij alle punten van de grafiek van \(f\) de \(x\)- en \(y\)-coördinaten te verwisselen. De grafieken zijn dus elkaar gespiegelden in de lijn \(y=x\).
Mathcentre videos
Composition of Functions (10:51)
#\phantom{x}#
Inverse Functions (17:57)


