Function definition and the argument of a function

Functions and graphs: Function machines and composition of functions

Function definition and the argument of a function

Function machine A function can be considered as a machine that processes input and produces output. We can visualise this machine as follows:

function machine

It is important here that the machine produces only one output for a given input and also that it always produces the same output when you offer the same input; only then is it a function machine. You can regard the prescription as a label on the machine that describes what it does.

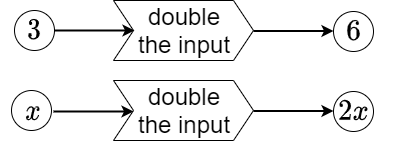
The following two pictures with specific inputs show how the function machine with the rule "double the input" works:

doubling machine

The prescription in this function machine can be cast in a formula-like form and given a name as follows:

verdubbelingsmachientje

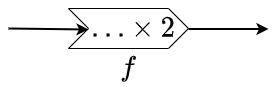
When inputting the number \(3\), this function machine returns the number \(6\) as output. Any input, say \(x\), yields the output \(2x\). In other words \(f(3)=6\) and \(f(x)=2x\). Mathematicians would rather stick the definition \(f(x)=2x\) as a label on the machine.

Naming functions Mathematicians often use the letters \(f\), \(F\), \(g\), \(G\), \(h\), and \(H\) for function names. But the letter \(y\) is also popular in combination with the letter \(x\) for the argument of the function, because a graph of such a function is drawn in the \(y\)-\(x\) plane.

Arrow notation for functions In order to retain the machine character of a function in the notation of a function definition, the arrow notation is sometimes used. In our example we write down \(f\,\mathrm{:}\,x\mapsto 2x\).

The argument of a function Given input of a function is also called the argument of the function; if it is a variable, it is also called the independent variable. You often want to calculate the function value, or also the dependent variable, via the function definition or function rule. For example, the function "double the input and add three" we can name \(y\) and define via the function \(y(t)=2t+3\) with an independent variable \(t\). In this example, the output \(y(4)\) is equal to \(2\times 4+3=8+3=11\). For any argument, say \(x\), then \(y(x)=2x+3\). If the argument is a mathematical formula, for example \(z+1\), then the output \(y(z+1)\) is equal to \(2\times (z+1)+3=2z+5\). In this case, the format \(y(z+1)\) does not represent a formula in two variables \(y\cdot(z+1)=y\cdot z + y\), but \(z+1\) is the argument of the function \(y\). Mathematical notation is often ambiguous if you don't consider the context!

We are not strict in the requirement that in a function rule every argument must lead to a function value; not everything you enter into a function machine may have meaning in the prescription and cause the machine to fail. A simple example is the machine with the rule "produce the reciprocal value of the given input", that is, the function \(f(x)=\frac{1}{x}\). If you enter the number \(0\), the machine fails.

A second example: with the function \(f(x)=\frac{x^2-1}{x-1}\), each \(x\neq 1\) leads to a value equal to the function value of \(g(x)=x-1\). For \(x=1\), function machine \(f\) fails, but not \(g\). Mathematicians say that the function \(f\) has a continuous continuation \(g\).