Functies en grafieken: Functiemachientjes en samenstelling van functies
 Functievoorschrift en het argument van een functie
Functievoorschrift en het argument van een functie
Functiemachientje Bij een functie kun je denken aan een machientje dat invoer verwerkt en uitvoer produceert. Dit machientje kunnen we als volgt visualiseren:

Hierbij is het wel belangrijk dat het machientje bij een gegeven invoer maar één uitvoer oplevert en ook dat het altijd dezelfde uitvoer oplevert wanneer je dezelfde invoer aanbiedt; pas dan is het een functiemachientje. Het voorschrift kun je als etiket op het machinetje beschouwen waarop beschreven staat wat het doet.
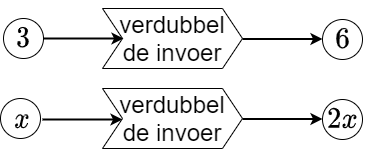
Onderstaande twee plaatjes met specifieke invoer tonen hoe het functiemachientje met als voorschrift "verdubbel de invoer" werkt:
Het voorschrift in dit functiemachientje kan als volgt in een formule-achtige vorm gegoten en van een naam voorzien worden:
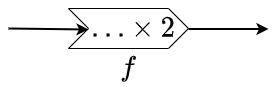
Dit functiemachientje levert bij invoer van het getal \(3\) als uitvoer het getal \(6\) op. Een willekeurige invoer, zeg \(x\), levert de uitvoer \(2x\) op. Met andere woorden \(f(3)=6\) en \(f(x)=2x\). Wiskundigen plakken dan liever als etiket op het machientje de definitie \(f(x)=2x\).
Het argument van een functie Gegeven invoer van een functie wordt ook wel het argument van de functie genoemd; als het een variabele is dan noemt men dit ook wel de onafhankelijke variabele. Vaak wil je dan de functiewaarde, of ook wel de afhankelijke variabele, berekenen via het functievoorschrift. Bijvoorbeeld, de functie "verdubbel de invoer en tel er drie bij op" kunnen we de naam \(y\) geven en via het functievoorschrift \(y(t)=2t+3\) met een onafhankelijke variabele \(t\) definiëren. In dit voorbeeld geldt dan dat de uitvoer \(y(4)\) gelijk is aan \(2\times 4+3=8+3=11\). Voor een willekeurige argument, zeg \(x\), geldt dan dat \(y(x)=2x+3\). Als het argument een wiskundige formule is, bijvoorbeeld \(z+1\), dan is de uitvoer \(y(z+1)\) gelijk aan \(2\times (z+1)+3=2z+5\). In dit geval staat de notatie \(y(z+1)\) dus niet voor een formule in twee variabelen \(y\cdot(z+1)=y\cdot z + y\), maar is \(z+1\) het argument van de functie \(y\). Wiskundige notatie is vaak ambigu als je de context niet in beschouwing neemt!


