Perforations, limits, and continuous or discontinuous functions

Functions and graphs: Properties of functions

Perforations, limits, and continuous or discontinuous functions

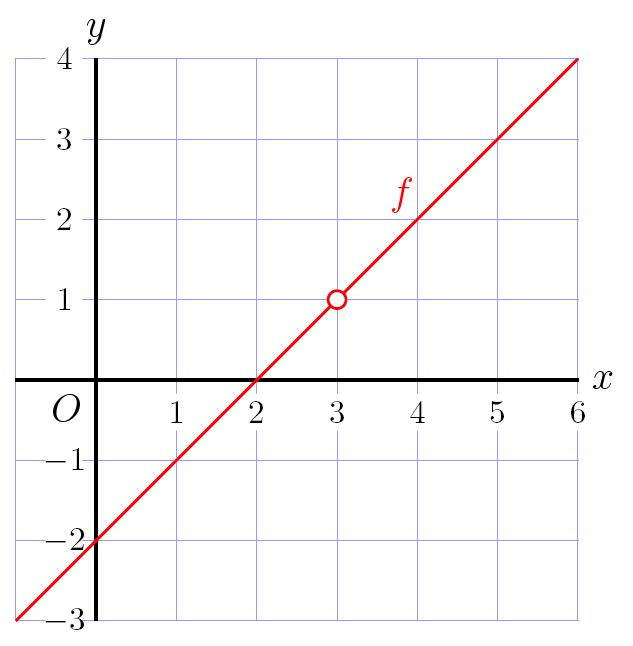
Have a look at the graph below of the function \(f(x)=\frac{x^2-5x+6}{x-3}\)

perforatie voorbeeld

The graph seems to be a straight line except at \(x=3\) because then things go horribly wrong, namely \(f(3)=\frac{3^2-5\times 3+6}{3-3}=\frac{0}{0}\) and this is undefined. The graph of \(f(x)\) therefore has a hole, or more formally stated, a perforation at \(x=3\). It is an example of a discontinuous function, loosely said a function in which one is at a certain moment forced to remove the tip of the pen from the paper when drawing the graph with pen and paper.

Near the perforation, the function behaves neatly. When we take \(x\) closer and closer to \(3\), \(f(x)\) will go more and more from \(1\). We say that \(f(x)\) goes to \(1\) when \(x\) goes to \(0\): \[f(x)\rightarrow 1\text{ when }x\rightarrow 3\] or that the limit of \(f(x)\) is \(1\) when \(x\) goes to \(0\): \[\lim_{x\to 3}f(x)=1\] We can see this by noting that \[f(x)=\frac{x^2-5x+6}{x-3}=\frac{(x-2)(x-3)}{x-3}=x-2\text{ subject to }x\neq 3\] The graph of \(g(x)=x-2\) is a straight line with slope \(1\) and vertical intercept \(-2\). With \(f(x)\) we are not allowed to enter \(x=3\), but with \(g(x)\) that is no problem and we get \(g(3)=1\). Using a limit we can determine the vertical value of the perforation: \[\begin{aligned}\lim_{x\to 3}f(x)&=\lim_{x\to 3}\frac{x^2-5x+6}{x-3}\\[0.25cm] &=\lim_{x\to 3}\frac{(x-2)(x-3)}{x-3}\\[0.25cm] &=\lim_{x\to 3}(x-2)\\[0.25cm] &=3-2\\[0.25cm] &=1\end{aligned}\] We can close the hole of \(f\) and make it a continuous function, loosely a function whose graph can be drawn with pen and paper without taking the tip of the pen off the paper. We construct a piecewise defined function, say \(F\), in the following way \[F(x)=\left\{\begin{array}{cl}\dfrac{x^2-5x+6}{x-3} & \text{voor } x\neq 3\\ 1&\text{for }x=3 \end{array}\right.\] The function \(F\) is then called the analytical continuation of the function \(f\).

With the loosely introduced limit concept, we can define the concept of perforation in the graph of a function and continuity somewhat more neatly.

Perforation of a function The graph of a function \(f\) has a perforation at the point \((a, b)\) if \(f(a)\) does not exist and \(\lim\limits_{x \to a} f(x)=b\).

Continuity of a function The function \(f(x)\) is called continuous in \(a\) if \(a\) is within the domain of \(f\), but not on the boundary of the definition area of \(f\), and if the limit \(\lim\limits_{x \to a}f(x)=f(a)\). A function is called continuous on an open interval \(I\) if \(I\) is part of the domain of \(f\) and if \(f\) is continuous at any point of \(I\).

We have excluded the boundary of the domain in this definition of continuity. This is not necessary, but then you must allow unilateral limits. The left limit and right limit can be introduced as follows.

The function \(f\) has in \(a\) a left limit \(\lim_{x\uparrow a}f(x)=L\) if \(f(x)\) goes to \(L\) as \(x\) goes from left to \(0\), i.e., you always assume that \(x<a\).
The function \(f\) has in \(a\) a right limit \(\lim_{x\downarrow}f(x)=L\) if \(f(x)\) goes to \(L\) as \(x\) goes from right to \(0\), ie you always assume that \(x>a\).

The function \(f(x)\) is called continuous from the left in \(a\) if \(a\) is within the domain of \(f\) and \(\lim_{x\uparrow a}f(x)=f(a)\).
The function \(f(x)\) is called continuous from the right in \(a\) if \(a\) is within the domain of \(f\) and \(\lim_{x\downarrow a}f(x)=f(a)\).

We can now also view the continuity of a function on a closed interval in the domain by limiting continuity in a left and right endpoint to continuity from right and left respectively.

Examples of commonly used discontinuous functions

Name	Definition	Graphic
step function, Heaviside function	\(H(x)=\left\{\begin{array}{rl} 1&\text{ for }x>0\\ 0 &\text{ for }x\le 0\end{array}\right.\)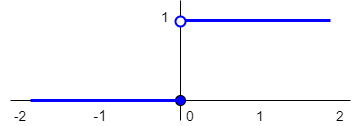
sign function	\(\mathrm{sign}(x)=\left\{\begin{array}{rl} 1&\text{ for }x>0\\ 0 &\text{ voor }x=0\\ -1 &\text{ voor }x< 0\end{array}\right.\)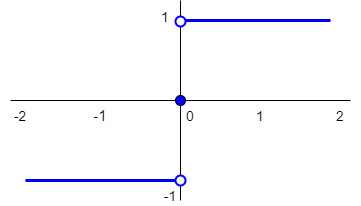
Dirac delta function	\(\delta(x)=\left\{\begin{array}{rl} 1&\text{ for }x=0\\ 0 &\text{ for }x\neq 0\end{array}\right.\)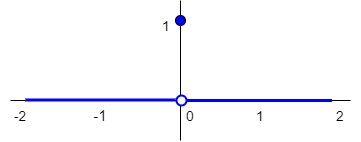