Perforaties, limieten en continue dan wel discontinue functies

Functies en grafieken: Kenmerken van functies

Perforaties, limieten en continue dan wel discontinue functies

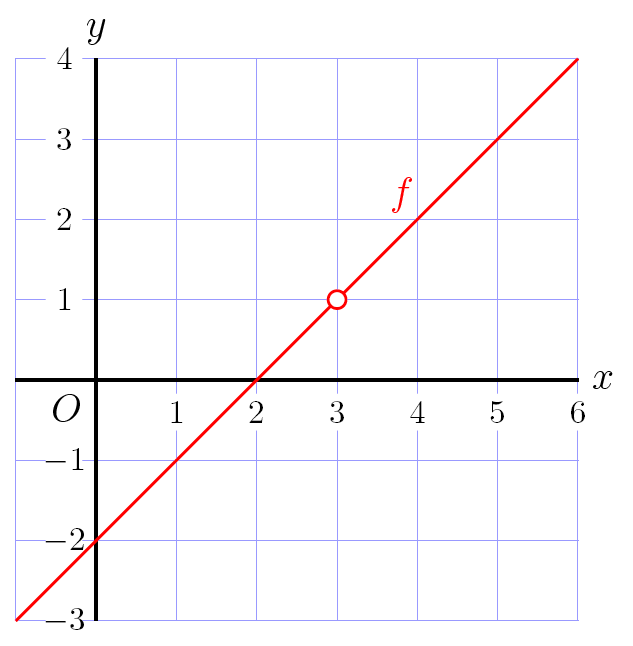
Bekijk onderstaande grafiek van de functie $f(x)=\frac{x^2-5x+6}{x-3}$

perforatie voorbeeld

De grafiek lijkt een rechte lijn behalve $x=3$ want dan gaat het gruwelijk mis, namelijk $f(3)=\frac{3^2-5\times 3+6}{3-3}=\frac{0}{0}$ en dit is niet gedefinieerd. De grafiek vaan $f(x)$ heeft in $x=3$ dus een gat, of deftiger gezegd een perforatie. Het is een voorbeeld van een discontinue functie, losjes gezegd een functie waarbij men bij het tekenen van de grafiek met pen en papier op een zeker moment genoodzaakt is om de pen van het papier af te halen.

In de buurt van de perforatie gedraagt de functie zich netjes. Als we $x$ steeds dichter bij $3$ kiezen, dan gaat $f(x)$ steeds meer van $1$ . We zeggen dat $f(x)$ naar $1$ gaat als $x$ naar $0$ gaat:

$f(x)\rightarrow 1\text{ als }x\rightarrow 3$ of dat de $f(x)$ de limiet $1$ heeft als $x$ naar $0$ gaat:

$\lim_{x\to 3}f(x)=1$ Dit kunnen we inzien door op te merken dat

$f(x)=\frac{x^2-5x+6}{x-3}=\frac{(x-2)(x-3)}{x-3}=x-2\text{ mits }x\neq 3$ De grafiek van $g(x)=x-2$ is een recht lijn is met helling $1$ en verticale asafsnede $-2$ . Bij $f(x)$ mogen we niet $x=3$ invullen, maar bij $g(x)$ is dat geen probleem en krijgen $g(3)=1$ . Met behulp van een limiet kunnen we de verticale waarde van de perforatie bepalen:

$\begin{aligned}\lim_{x\to 3}f(x)&=\lim_{x\to 3}\frac{x^2-5x+6}{x-3}\\[0.25cm] &=\lim_{x\to 3}\frac{(x-2)(x-3)}{x-3}\\[0.25cm] &=\lim_{x\to 3}(x-2)\\[0.25cm] &=3-2\\[0.25cm] &=1\end{aligned}$ We kunnen het gat van $f$ dichtmaken en er een continue functie van maken, losjes gezegd een functie waarvan de grafiek met pen en papier getekend kan worden zonder de pen van het papier te hoven halen. We construeren dan een stuksgewijs gedefinieerde functie, zeg $F$ , op de volgende manier

$F(x)=\left\{\begin{array}{cl}\dfrac{x^2-5x+6}{x-3} & \text{voor } x\neq 3\\ 1&\text{voor }x=3 \end{array}\right.$ De functie $F$ heet dan een continue voortzetting van de functie $f$ .

Met het losjes geïntroduceerde limietbegrip kunnen we het begrip perforatie in de grafiek van een functie en continuïteit wat netter definiëren.

De grafiek van een functie $f$ heeft een perforatie in het punt $(a, b)$ als $f(a)$ niet bestaat en $\lim\limits_{x \to a} f(x)=b$ .

De functie $f(x)$ heet continu in $a$ als $a$ in het domein van $f$ ligt, maar niet op de rand van het definitiegebied van $f$ , en als de limiet $\lim\limits_{x \to a}f(x)=f(a)$ . Een functie heet continu op een open interval $I$ als $I$ deel uitmaakt van het domein van $f$ en als $f$ continu is in elk punt van $I$ .

We hebben in deze definitie van continuïteit de rand van het domein uitgesloten. Dit hoeft niet maar dan moet je eenzijdige limieten toestaan. De linkerlimiet en rechterlimiet kunnen als volgt geïntroduceerd worden.

De functie $f$ heeft in $a$ een linkerlimiet $\lim_{x\uparrow a}f(x)=L$ als $f(x)$ naar $L$ gaat als $x$ van links naar $0$ gaat, d.w.z. je veronderstelt steeds dat $x<a$ .
De functie $f$ heeft in $a$ een rechtlimiet $\lim_{x\downarrow}f(x)=L$ als $f(x)$ naar $L$ gaat als $x$ van rechts naar $0$ gaat, d.w.z. je veronderstelt steeds dat $x>a$ .

De functie $f(x)$ heet continu van links in $a$ als $a$ in het domein van $f$ ligt en $\lim_{x\uparrow a}f(x)=f(a)$ .
De functie $f(x)$ heet continu van rechts in $a$ als $a$ in het domein van $f$ ligt en $\lim_{x\downarrow a}f(x)=f(a)$ .

We kunnen nu ook de continuïteit van een functie op een gesloten interval in het domein bekijken door continuïteit in een linker- en rechtereindpunt te beperken tot continuïteit van rechts respectievelijk van links.

Voorbeelden van veelgebruikte discontinue functies

Naam	Definitie	Grafiek
stapfunctie, Heaviside functie	$H(x)=\left\{\begin{array}{rl} 1&\text{ voor }x>0\\ 0 &\text{ voor }x\le 0\end{array}\right.$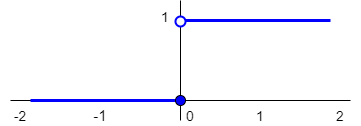
tekenfunctie	$\mathrm{teken}(x)=\left\{\begin{array}{rl} 1&\text{ voor }x>0\\ 0 &\text{ voor }x=0\\ -1 &\text{ voor }x< 0\end{array}\right.$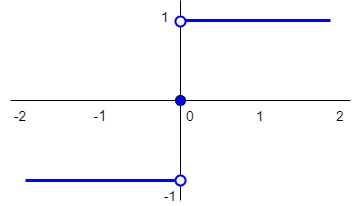
Dirac delta functie	$\delta(x)=\left\{\begin{array}{rl} 1&\text{ voor }x=0\\ 0 &\text{ voor }x\neq 0\end{array}\right.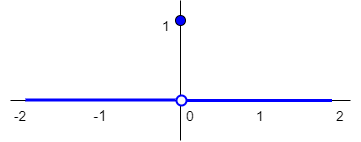$