Functions and graphs: Properties of functions
 Periodic functions
Periodic functions
Any function that has a pattern that repeats at regular intervals is called a periodic function. The length of the smallest intervals at which the periodic function repeats itself is called the period and is often denoted by the letter \(T\). \[\text{In case of a periodic function }F(t)\text{ with period }T\text{ it is true that } F(t+T)=F(t)\text{ for all }t\text.\]
In a periodic function that depends on time, the frequency is defined as the number of periods per unit of time and denoted by the letter \(f\); the frequency is then the reciprocal value of the period, i.e., in formula \(f=\dfrac{1}{T}\).
We give a few examples of periodic functions.
Movement of a point over the edges of a square A point \(P\) moves over the edges of the tilted square below. This point starts in \((2,0)\) and moves counterclockwise. Next to the square is the graph of the height of \(P\) versus the distance travelled by \(P\). In blue we have indicated the part of the graph that is repeated during the movement of the point \(P\). The period of the matching function is equal to \(16\).

Movement of a point over the edges of a tilted square A point \(P\) moves over the edges of the tilted square below. This point starts in \((2,0)\) and moves counterclockwise. Next to the square is the graph of the height of \(P\) versus the distance traveled by \(P\). The period of the matching function is equal to \(8\sqrt{2}\).

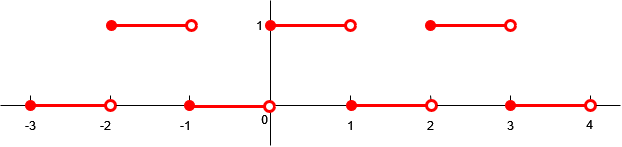
Periodic continuation of the function Consider the function \[f(x)=\begin{cases} 1& \text{for }0\le x<1\\ 0& \text{for }1\le x< 2\end{cases}\] This function is thus defined on the interval \([0,2)\) and the graph consists of two horizontal line segments of length 1 each with a closed and open edge point. You can shift a copy of this graph to the right by a distance 2, a second copy by a distance 4 to the right, and so on. You can also shift to the left over these distances. In this way you repeat the pattern to the left and to the right and you get the graph of a periodic function that is defined for all real numbers. Part of the graph of this function is plotted below on the interval \([-3,4)\). The constructed periodic function is called the periodic continuation of \(f\).
Equilibrium value and amplitude In the graphs above, the function values fluctuate around an equilibrium value. The equilibrium value can be determined by figuring out what the average value of the function is over one period. The amplitude is then the maximum deviation from the equilibrium value.
Due to the symmetry in the top two graphs, it is understandable that in these examples the equilibrium value is equal to zero; the amplitude is equal to \(2\) in both examples.
In the third graph above, the equilibrium value and amplitude are equal to \(\dfrac{1}{2}\).


