Periodieke functies

Functies en grafieken: Kenmerken van functies

Periodieke functies

Elke functie die een patroon heeft dat herhaald wordt op regelmatige intervallen noemen we een periodieke functie. De lengte van de kleinste intervallen waarop de periodieke functie zich herhaald heet de periode en wordt vaak met de letter $T$ aangeduid.

$\text{In het geval van een periodieke functie }F(t)\text{ met periode }T\text{ geldt dat } F(t+T)=F(t)\text{ voor alle }t\text.$

Bij een periodieke functie die van tijd afhangt wordt de frequentie gedefinieerd als het aantal perioden per eenheid van tijd en aangeduid met de letter $f$ ; de frequentie is dan de reciproque waarde van de periode, oftewel in formuletaal $f=\dfrac{1}{T}$ .

We geven een paar voorbeelden van periodieke functies.

Over de rand van onderstaand gekanteld vierkant beweegt een punt $P$ . Dit punt start in $(2,0)$ en beweegt linksom. Naast het vierkant staat de grafiek van de hoogte van $P$ uitgezet tegen de afgelegde afstand van $P$ . In blauw hebben we het stukje van de grafiek aangeduid dat steeds herhaald wordt tijdens de beweging van het punt $P$ . De periode van de bijpassende functie is gelijk aan $16$ .

voorbeeld 1 van een periodieke functie

Over de rand van onderstaand vierkant beweegt een punt $P$ . Dit punt start in $(2,0)$ en beweegt linksom. Naast het vierkant staat de grafiek van de hoogte van $P$ uitgezet tegen de afgelegde afstand van $P$ . De periode van de bijpassende functie is gelijk aan $8\sqrt{2}$ .

voorbeeld 2 van een periodieke functie

Periodieke voortzetting van de functie Beschouw de functie

$f(x)=\begin{cases} 1& \text{voor }0\le x<1\\ 0& \text{voor }1\le x< 2\end{cases}$ Deze functie is dus gedefinieerd op het interval $[0,2)$ en de grafiek bestaat uit twee horizontale lijnstukjes van lengte 1 met steeds een gesloten en open randpunt. Een kopie van deze grafiek kun je verschuiven naar rechts over een afstand 2, een tweede kopie over een afstand 4 naar rechts, enzovoort. Ook kun je over deze afstanden naar links verschuiven. Zo herhaal je het patroon naar links en naar rechts en krijg je de grafiek van een periodiek functie die voor alle reële getallen gedefinieerd is. Een deel van de grafiek van deze functie is hieronder getekend op het interval $[-3,4)$ , De geconstrueerde periodieke functie heet de periodieke voortzetting van $f$ .

voorbeeld 3 van een periodieke functie

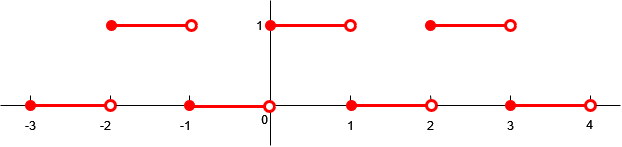
Evenwichtsstand en amplitude In bovenstaande grafieken schommelen de functiewaarden om een evenwichtsstand. De evenwichtsstand kan bepaald worden door uit te zoeken wat de gemiddelde waarde van de functie is over één periode. De amplitude is dan de maximale afwijking van de evenwichtsstand.

Vanwege de symmetrie in de bovenste twee grafieken is te begrijpen dat in deze voorbeelden de evenwichtsstand gelijk is aan nul; de amplitude is in beide voorbeelden gelijk aan $2$ .
In de laatste grafiek zijn de evenwichtsstand en amplitude gelijk aan $\dfrac{1}{2}$ .