Functions and graphs: Properties of functions
 Even and odd functions
Even and odd functions
Have a look at the following series of graphs of functions? What do they have in common?
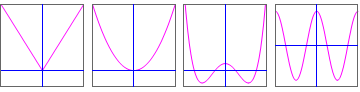
Now take a look at the following series of graphs of functions? What do these graphs have in common?
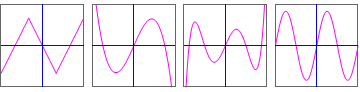
Hopefully you have seen that the graph in the first series is symmetrical to the vertical axis, i.e., the piece of the graph to the left of the vertical axis is the mirror image of the piece of the graph to the right of the vertical axis.
In the second series of graphs there is rotational symmetry around the origin of the coordinate system: when you rotate the graph 180 degrees around the origin, you get the same graph.
A function \(f\) has even when \(f(-x)=f(x)\) for any argument \(x\). The graph of an even function \(f(x)\) is symmetric with respect to the \(x=0\) axis, i.e., with the vertical axis. This means that if you replace an argument with its opposite, the function value does not change.
A function \(f\) has odd when \(f(-x)=-f(x)\) for any argument \(x\). The graph of an odd function \(f(x)\) is antisymmetric to the \(x=0\) axis, i.e., to the vertical axis. This means that you get the opposite function value if you replace an argument with its opposite. This also means that the graph is rotationally symmetric about the origin, ie after rotation of the graph by 180 degrees around the origin the same graph is created.
Examples of even functions
\[|x|, x^2, x^4\text{ and }\cos(x)\]
Examples of odd functions
\[x, x^3\text{ and }\sin(x)\]


