Functies en grafieken: Kenmerken van functies
 Even en oneven functies
Even en oneven functies
Kijk eens naar onderstaande reeks van grafieken van functies? Wat hebben ze met elkaar gemeen?
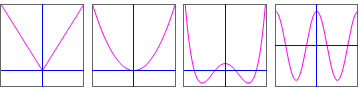
Kijk nu eens naar onderstaande reeks van grafieken van functies? Wat hebben deze grafieken met elkaar gemeen?
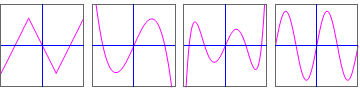
Hopelijk heb je gezien dat de grafiek in de eerste reeks symmetrisch zijn t.o.v. de verticale as, d.w.z. het stukje van de grafiek links van de verticale as is het spiegelbeeld van het stukje van de grafiek rechts van de verticale as.
In de tweede reeks van grafieken is er sprake van rotatie-symmetrie rondom de oorsprong van het assenstelsel: als je de grafiek 180 graden draait rondom de oorsprong, dan krijg je dezelfde grafiek.
Een functie \(f\) heeft even als \(f(-x)=f(x)\) voor elke argument \(x\). De grafiek van een even functie \(f(x)\) is symmetrisch t.o.v. de \(x=0\) as, d.w.z. de verticale as. Dit betekent dat de functiewaarde niet wijzigt als je een argument vervangt door zijn tegengestelde.
Een functie \(f\) heeft oneven als \(f(-x)=-f(x)\) voor elke argument \(x\). De grafiek van een oneven functie \(f(x)\) is antisymmetrisch t.o.v de \(x=0\) as, d.w.z. de verticale as. Dit betekent dat je de tegengestelde functiewaarde krijgt als je een argument vervangt door zijn tegengestelde. Ook betekent dit dat de grafiek van rotatie-symmetrisch is om de oorsprong, d.w.z dat na draaiing van de grafiek over 180 graden rondom de oorsprong dezelfde grafiek ontstaat.
Voorbeelden van even functies
\[|x|, x^2, x^4\text{ en }\cos(x)\]
Voorbeelden van oneven functies
\[x, x^3\text{ en }\sin(x)\]


