Grafiek van een functie

Functies en grafieken: Data en grafieken

Grafiek van een functie

De meeste functies die je tegenkomt zijn "gladde" functies, d.w.z. functies met vloeiende krommen als grafieken. Om de grafiek van een dergelijke functie, zeg $f$ , te tekenen volstaat om een voldoende aantal functiewaarden $f(x)$ voor verschillende argumenten $x$ uit te rekenen en dan de berekende punten $\bigl(x,f(x)\bigr)$ als punten op de grafiek in het vlak te tekenen. Daarna rest je nog alleen om bij opklimmende argumenten van de functie $f$ opeenvolgende punten met elkaar te verbinden via rechte lijnstukken of zelfs via gekromde lijnstukjes om hoekige grafieken te voorkomen.

Om het gedrag van een functie in grafiekvorm goed in beeld te krijgen moet je letten op bijzondere punten. Dat zijn bijvoorbeeld:

punten op of dicht bij de rand van het domein van een functie;
punten in de omgeving waarvan de functie een maximum of minimum aanneemt;
asafsnedes, d.w.z punten waar de grafiek de horizontale of verticale as van het assenstelsel snijdt;
punten waar de functie niet gedefinieerd is of het functievoorschrift wijzigt.

Als het functievoorschrift van een bekende vorm is, bijvoorbeeld een lineaire functie, dan kun je teren op kennis die je over zo'n functie al eerder hebt opgedaan hebt. Maar in het algemeen zul je voor het tekenen van een grafiek van een functie vaak eerst een functieonderzoek moeten doen. Een groot deel van Calculus gaat over het doen van goed functieonderzoek.

We bekijken de kwadratische functie $f(x)=(x-1)^2-1$ en willen de grafiek tekenen op het interval $[-1,3]$ .

De punten op randen van dit interval zijn eenvoudig uit te rekenen: het zijn de punten $(-1,3)$ en $(3,3)$ omdat $f(-1)=f(3)=3$ .

Een kwadraat van een reëel getal is altijd een niet-negatief getal en gelijk aan nul voor het getal $0$ . Daarom is het punt $(1,-1)$ een punt van de grafiek dit het laagst in het vlak ligt. Daar neemt de functie een minimale waarde aan.

Asafsnedes met de horizontale as vind je door de vergelijking $f(x)=0$ op te lossen, in dit geval door $x$ te bepalen waarvoor $(x-1)^2-1=0$ . Dan moet gelden $(x-1)^2=1$ oftewel $x-1=\pm 1$ . Dus: $x=0$ of $x=2$ . De grafiek van $f$ snijdt de horizontale as in de punten $(0,0)$ en $(2,0)$ . In dit voorbeeld is de asafsnede met de verticale as ook gelijk bekend.

Een belangrijke eigenschap van de functie is dat $f(1+x)=f(1-x)$ voor elk getal $x$ . Ga maar na: $f(1+x)=x^2-1=(-x)^2-1=f(1-x)$ . Dit betekent dat de grafiek van $f$ symmetrisch is t.o.v. de verticale lijn $x=1$ , d.w.z. dat de grafiek gelijk blijft als je deze spiegelt in de verticale lijn $x=1$ . Met andere woorden, als je weet hoe de grafiek er uit ziet op het deelgebied $[1,3]$ , dan kun je door spiegelen ook de grafiek tekenen op het deelgebied $[-1,1]$ .

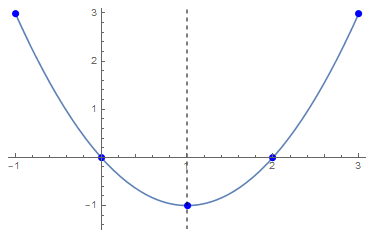
Hiermee is al best veel bekend geworden over de grafiek om deze te kunnen tekenen. Hieronder staat het computer-gegenereerde diagram. De speciale punten en de gestippelde symmetrie-as zijn er ook in getekend.

grafiek van een kwadratische functie

De grafiek van een functie $f$ is de verzameling geordende paren $(x,y)$ waarvoor $y=f(x)$ . Als $x$ en $y$ reële getallen zijn kun je het paar opvatten als coördinaten van punten in $\mathbb{R}^2$ . Een meer formele definitie van de grafiek van een functie luidt als volgt:

Laat $D$ een deelverzameling van $\mathbb R$ zijn. De grafiek van een functie $f\,\text{:}\,D\to\mathbb{R}$ is de verzameling $\left\{\bigl(x,f(x)\bigr)\in D\times\mathbb{R}\mid x\in D\right\}\text{.}$ Deze grafiek wordt zichtbaar gemaakt door deze verzameling van punten in $\mathbb{R}^2$ te tekenen in het reële vlak.

$D$ is in bovenstaande definitie een symbool voor een deelverzameling van $\mathbb R$ . Vaak is dit een interval of het domein van de functie in kwestie, maar dat hoeft niet per se zo te zijn.

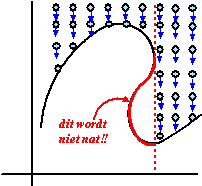
Als we een grafiek definiëren als een deelverzameling van ${\mathbb R}^2$ , dan is duidelijk dat elke grafiek van een functie inderdaad een grafiek is. Maar het omgekeerde is niet waar. De cirkel met de oorsprong als centrum en straal $1$ kunt je beschrijven als $\{(x,y)\in\mathbb{R}^2\mid x^2+y^2=1\}$ , maar dit is niet de grafiek van een functie $f$ . Voor elke $x$ uit het interval $(-1,1)$ zouden dan twee functiewaarden moet bestaan, namelijk $\pm\sqrt{1-x^2}$ , maar dat is niet toegestaan in een functie. Een functie moet bij een gegeven argument hoogstens één waarde opleveren.

De grafiek van een functie herkennen De grafiek van een functie heeft de volgende eigenschap:

Als $(x,y)$ en $(x,z)$ elementen uit de grafiek van een functie zijn, dan geldt dat $y=z$ .

Omgekeerd, als een grafiek deze eigenschap heeft, dan is het ook de grafiek van een functie.

Als er bij elke $x$ hoogstens één $y$ bij de grafiek van een functie mag horen, dan heeft dus elke verticale lijn hoogstens één snijpunt met de grafiek van de functie. Daarom spreekt men van het verticale-lijn criterium Dit impliceert dat de grafiek van een functie niet mag "teruglopen" of "omkeren". Henk Hofstede introduceert op zijn website met lesmateriaal het volgende ezelsbruggetje om het criterium te onthouden: "Als het regent wordt een functie helemaal nat". Hij visualiseert dit met onderstaande figuur als voorbeeld van een grafiek die geen grafiek van een functie is.

grafiek, maar geen functiegrafiek