Functies en grafieken: Data en grafieken
Assenstelsel
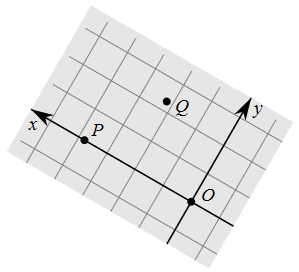
Scheef assenstelsel De plaats van een punt op een blad papier o fin een plat vlak kan worden aangegeven met behulp van twee getallen. Maar daarvoor moet je eerst een assenstelsel creëren. Daarvoor heb je drie punten, zeg \(O\), \(Q_1\) en \(Q_2\), nodig die niet op één lijn liggen. Het punt \(O\) kiezen we als oorsprong in het vlak. De lijn \(OQ_1\) kunnen we als eerste coördinaatas gebruiken, en de lijn \(OQ_2\) kunnen we als tweede coördinaatas gebruiken; de oorsprong is het snijpunt van deze twee lijnen. De punten \(Q_1\) en \(Q_2\) kunnen we dan respectievelijk de coördinaten \((1,0)\) en \((0,1)\) geven. Elk punt \(P\) in het vlak kunnen we nu schrijven als punt van een parallellogram met twee zijden langs de coördinaatassen, waarvan de lengtes veelvouden zijn van de lengtes van de lijnstukken \(OQ_1\) en \(OQ_2\). De scalairen zijn de coördinaten van het punt \(P\). Zie onderstaande figuur met een scheef assenstelsel.
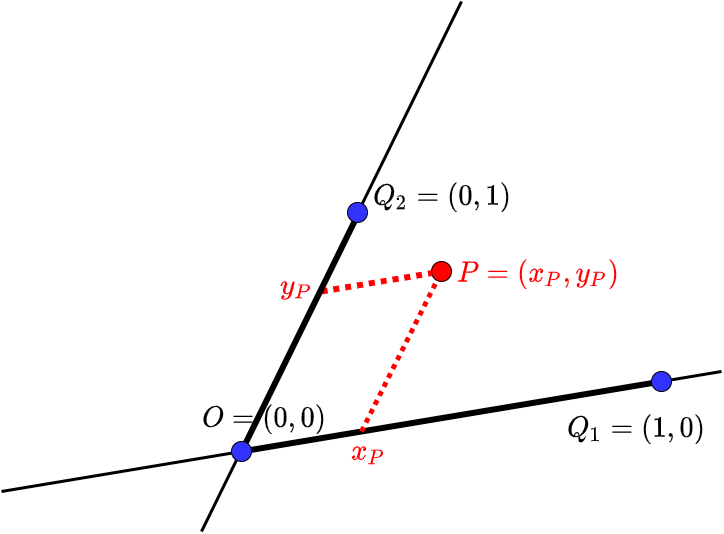
De coördinaatasssen in dit assenstelsel kunnen we opvatten als getallenlijnen en elk getal op een coördinaatas correspondeert dan met een punt op de as.
Scheef ruitjespapier De punten in het vlak met gehele coördinaten vormen samen een rooster. In onderstaande figuur zijn ook de roosterlijnen getekend zodat je scheef ruitjespapier krijgt (de turquoise kleuring is er alleen ter versiering).
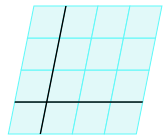
Rechthoekig assenstelsel In een rechthoekig assenstelsel, deftiger Cartesisch assenstelsel genoemd, staan de coördinaatassen onderling loodrecht op elkaar en is het lengtebegrip langs beide assen gelijk gekozen. In onderstaande figuur zijn twee pijlen in blauw en rood getekend met het de pijlpunten eindigend in de punten met coördinaten \((1,0)\) en \((0,1)\) De punten in het vlak met gehele coördinaten vormen samen een rooster. In onderstaande figuur zijn ook de roosterlijnen getekend zodat je ruitjespapier krijgt (de turquoise kleuring is er alleen ter versiering).
Constructie van een Cartesisch assenstelsel bij drie punten Een Cartesisch assenstelsel kunnen we in het platte vlak naar eigen keuze vastleggen. Dit kunnen we bij elk drietal punten, zeg \(O\), \(P\) en \(Q\), nodig die niet op één lijn liggen zodanig doen dat
- het punt \(O\) coördinaten \((0,0)\) heeft,
- het punt \(P\) de coördinaten \((p,0)\) heeft voor zekere \(p>0\),
- het punt \(Q\) de coördinaten \((q_1, q_2)\) heeft voor zekere \(q_1 \) en \(q_2\) met \(q_2 > 0\).
Zie onderstaande figuur.
Op schaling na is dit Cartesische assenstelsel uniek. Zo'n constructie van een Cartesisch assenstelsel helpt om meetkundige problemen te vertalen naar problemen die zich in coördinaten laten beschrijven en hiermee op te lossen zijn.
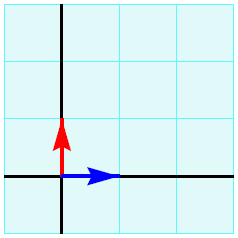
Met een keuze van een Cartesisch assenstelsel in een vlak krijgen we een coördinaatvlak dat we met \(\mathbb{R}^2\) aanduiden.
Een rechthoekig assenstelsel met verschillende horizontale en verticale schaling In een rechthoekig assenstelsel heb je assen in de vorm van getallenlijnen met het getal \(0\) bij de oorsprong van het assenstelsel. Bij de horizontale as staan de positieve getallen rechts van de oorsprong en de negatieve getallen links; bij de verticale as staan de positieve getallen boven de oorsprong en de negatieve getallen eronder. De eenheden, d.w.z. de afstanden tussen opeenvolgende getallen, op de horizontale en verticale assen zijn bij voorkeur even groot, maar dit is niet noodzakelijk. Zie onderstaande grafiek van \(f(x)= x^5-5x^3-x^2+4x+2\) over het interval \([-2.4,2.4]\) met een verticaal tekengebied van\([-4.8,4.8]\), zodanig gekozen dat je een goed beeld van de grafiek van de functie krijgt.
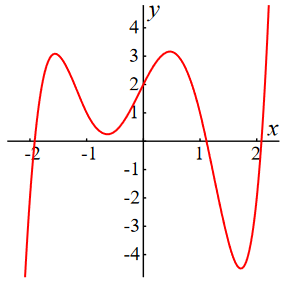
Om de positie van een punt vast te leggen, ga je na hoeveel je vanuit de oorsprong naar rechts (of naar links) en naar boven (of beneden) moet gaan om bij dat punt aan te komen.
Schaalaanduidingen aan de zijkanten van een diagram Omdat de assen in een rechthoekig assenstelsel wel eens een goed beeld van grafieken in de weg staan, worden ze soms weggelaten. Maar dan zijn de schaalaanduidingen aan de zijkanten van het diagram wel zichtbaar. Dit helpt ook als het tekengebied uit sterk verschillende intervallen op de horizontale en verticale as bestaat.
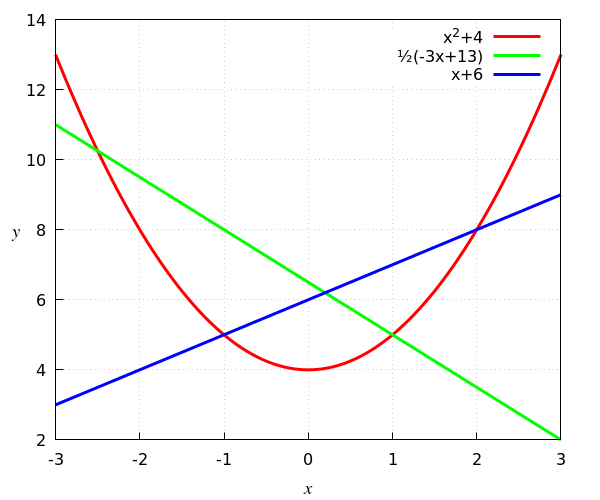
In onderstaande figuur zijn de grafieken van de functie \(x\mapsto x^2+4\), \(x\mapsto \tfrac{1}{2}(-3x+13)\) en \(x\mapsto x+6\) in één figuur getekend. Om de positie van een punt op de grafiek te bepalen, ga je verticaal naar beneden om de \(x\)-coördinaat van het punt op de horizontale schaal af te lezen en horizontaal naar links om de \(y\)-coördinaat van het punt op de verticale schaal af te lezen. Je kunt dus aflezen dat in dit voorbeeld \((2,8)\) een gemeenschappelijk punt op de rode en blauwe grafiek is, d.w.z. een snijpunt van de functies \(x\mapsto x^2+4\) en \(x\mapsto x+6\) is.
In de figuur is ook een bijschrift rechtsboven opgenomen dat aangeeft welke kromme bij welk functievoorschrift past. Dit heet een legenda bij het diagram.
