Functions and graphs: Transformations of graphs and functions
Vertical multiplication
Vertical multiplication For any function \(f\) and any number \(a\neq 0\), the graph of the function \(g\) defined by \(g(x)=a\cdot f(x)\) is obtained from the graph of \(f\) by multiplying it vertically by \(a\): the vertical coordinate is multiplied by \(a\).
If \(a>0\), then it is stretching or shrinking the graph relative to the horizontal axis.
If \(a<0\), then all points will be on the other side of the horizontal axis.
A special case is \(a=-1\): then the graph of \(f\) mirrored in the horizontal axis.
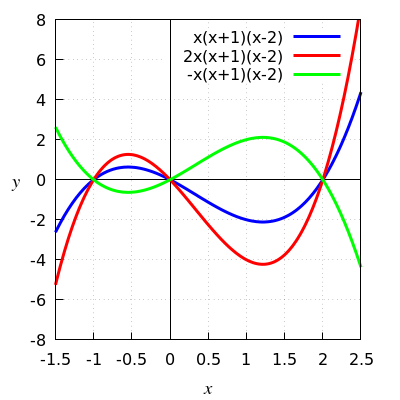
The figure below shows the graphs of \(x\mapsto x(x+1)(x-2)\), \(x \mapsto 2x(x+1)(x-2)\) and \(x \mapsto -x(x+1)(x-2)\).
The red graph of \(x \mapsto 2x(x+1)(x-2)\) is obtained by stretching the blue graph of \(x\mapsto x(x+1)(x-2)\) vertically by a factor of \(2\) ( \(a=2\) ).
You get the green graph of \(x \mapsto -x(x+1)(x-2)\) by mirroring the blue graph of \(x\mapsto x(x+1)(x-2)\) in the horizontal ( \(a=-1\) ).
