Functies en grafieken: Transformaties van grafieken en functies
Horizontaal vermenigvuldigen
Horizontale vermenigvuldiging Voor elke functie \(f\) en elk getal \(b\neq 0\) wordt de grafiek van de functie \(g\) gedefinieerd door \(g(x)= f(b\cdot x)\) verkregen uit de grafiek van \(f\) door deze horizontaal met \(1/b\) te vermenigvuldigen: de horizontale coördinaat wordt met \(1/b\) vermenigvuldigd.
Als \(b>0\), dan gaat het om uitrekken of krimpen van de grafiek t.o.v. de verticale as.
Als \(b<0\), dan komen alle punten aan de andere kant van de verticale as te liggen.
Een speciaal geval is \(b=-1\): dan wordt de grafiek van \(f\) gespiegeld in de verticale as.
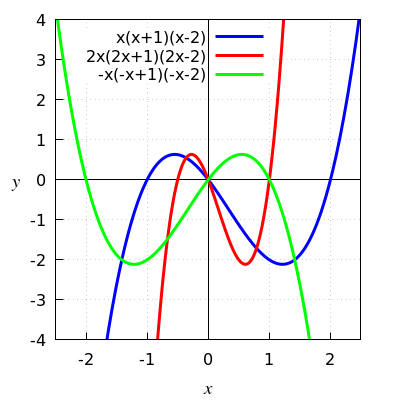
In onderstaande figuur staan de grafieken van \(x\mapsto x(x+1)(x-2)\), \(x \mapsto 2x(2x+1)(2x-2)\) en \(x \mapsto -x(-x+1)(-x-2)\).
De rode grafiek van \(x \mapsto 2x(2x+1)(2x-2)\) krijg je door de blauwe grafiek van \(x\mapsto x(x+1)(x-2)\) horizontaal met een factor \(\frac{1}{2}\) te vermenigvuldigen
De groene grafiek van \(x \mapsto -x(-x+1)(-x-2)\) krijg je door de blauwe grafiek van \(x\mapsto x(x+1)(x-2)\) te spiegelen in de verticale as.
