Functions and graphs: Transformations of graphs and functions
Combination of transformations
The four transformations discussed earlier, namely vertical translation, horizontal translation, vertical multiplication, and horizontal multiplication, can also be combined. The most common transform is \(g(x)=a\cdot f\bigl(b\cdot x+c\bigr)+d\) for a given function \(f(x)\).
Here, the graph of \(f\) is first transated horizontally by \(c\). A horizontal multiplication by \(1/b\) is then applied to the result. Vertical multiplication by \(a\) is applied to this intermediate result and then a vertical translation by \(d\).
Note: the order of application of the four transformations matters. For example, if you first multiply the function \(f(x)\) by \(b\) and then shift it by \(c\), you get \(x\mapsto f\bigl(b\cdot(x+c)\bigr)\).
Sketch the graph of the function \(x\mapsto \tfrac{1}{2} \sqrt{2x-3}+2\) based on the graph of the square root function.
We show step by step which transformations we successively apply to a graph; the gray graph is always the red result obtained in the previous step.
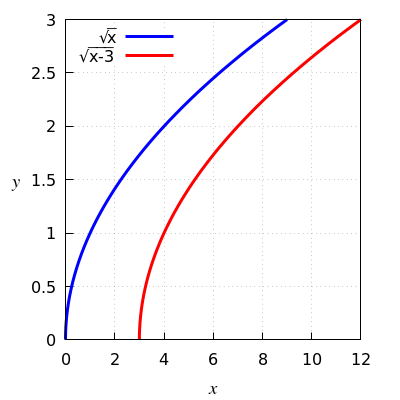
Function rule from \(\sqrt{x}\) to \(\sqrt{x-3}\)
Start with the graph of the square root function and move it by three to the right.
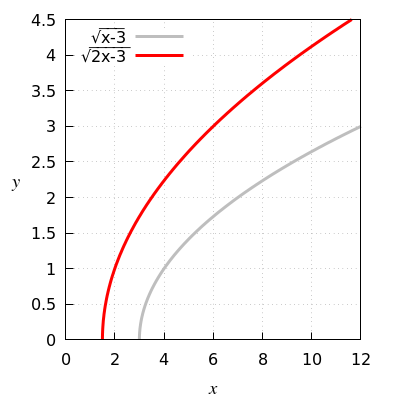
Function rule from \(\sqrt{x-3}\) to \(\sqrt{2x-3}\)
Multiply the gray graph horizontally by the factor \(\frac{1}{2}\).
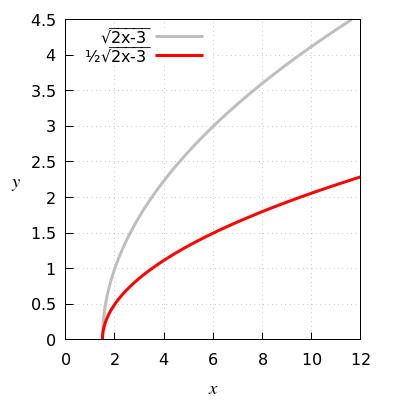
Function rule from \(\sqrt{2x-3}\) to \(\tfrac{1}{2}\sqrt{2x-3}\)
Multiply the gray graph vertically by the factor \(\tfrac{1}{2}\).
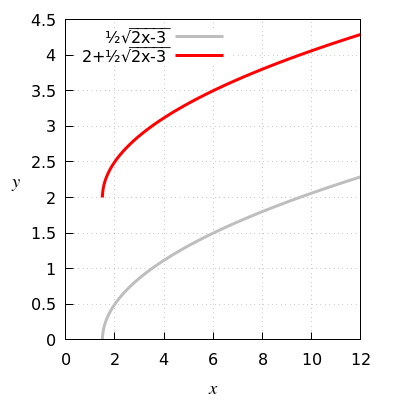
Function rule from \(\tfrac{1}{2}\sqrt{2x-3}\) to \(\tfrac{1}{2}\sqrt{2x-3}+2\)
Move the gray graph upward with \(2\).
