Functies en grafieken: Transformaties van grafieken en functies
 Combinatie van transformaties
Combinatie van transformaties
De vier eerder besproken transformaties, te weten verticaal verschuiven, horizontaal verschuiven, verticaal vermenigvuldigen en horizontaal vermenigvuldigen, kunnen ook gecombineerd worden. De meest algemene transformatie is \(g(x)=a\cdot f\bigl(b\cdot x+c\bigr)+d\) voor een gegeven functie \(f(x)\).
Hier wordt eerst de grafiek van \(f\) horizontaal verschoven met \(c\). Op het resultaat wordt daarna een horizontale vermenigvuldiging met \(1/b\) toegepast. Op dit tussenresultaat wordt verticale vermenigvuldiging met \(a\) toegepast en vervolgens nog een verticale verschuiving met \(d\).
Let op: de volgorde van toepassing van de vier transformatie doet er toe. Als je bijvoorbeeld eerst de functie \(f(x)\) vermenigvuldigt met \(b\) en daarna met \(c\) verschuift dan krijg je \(x\mapsto f\bigl(b\cdot(x+c)\bigr)\).
Schets de grafiek van de functie \(x\mapsto \tfrac{1}{2} \sqrt{2x-3}+2\) op basis van de grafiek van de wortelfunctie.
We laten stap voor stap zien welke transformaties we achtereenvolgens toepassen op een grafiek; de grijze grafiek is hierbij steeds het rode resultaat verkregen in de vorige stap.
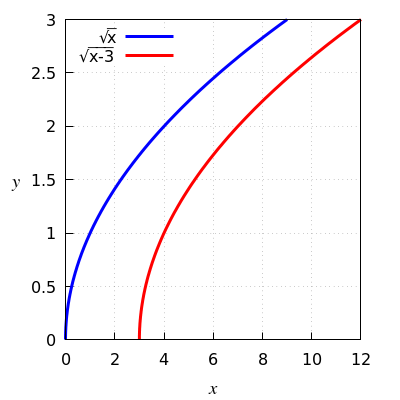
Functievoorschrift van \(\sqrt{x}\) naar \(\sqrt{x-3}\)
Start met de grafiek van de wortelfunctie en verschuif die met drie naar rechts.
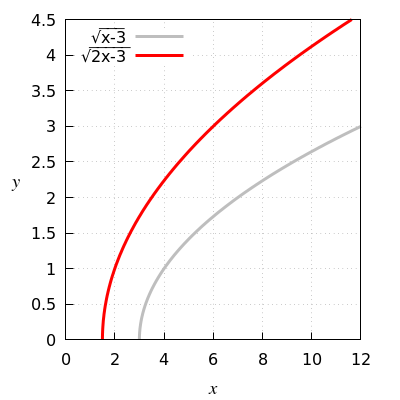
Functievoorschrift van \(\sqrt{x-3}\) naar \(\sqrt{2x-3}\)
Vermenigvuldig de grijze grafiek horizontaal met factor \(\frac{1}{2}\)
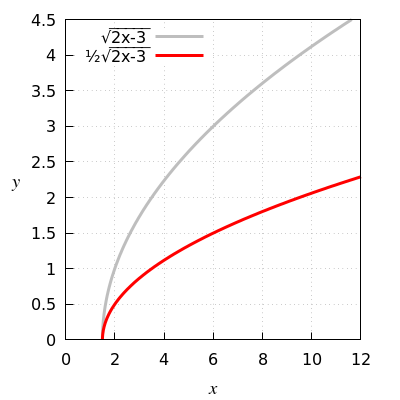
Functievoorschrift van \(\sqrt{2x-3}\) naar \(\tfrac{1}{2}\sqrt{2x-3}\)
Vermenigvuldig de grijze grafiek verticaal met de factor \(\tfrac{1}{2}\).
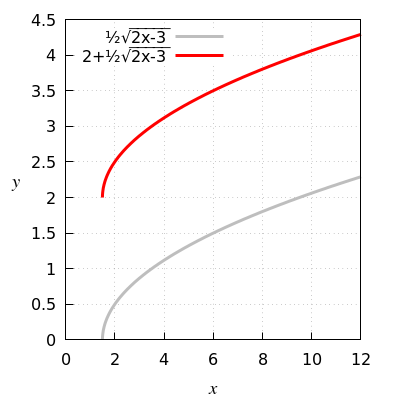
Functievoorschrift van \(\tfrac{1}{2}\sqrt{2x-3}\) naar \(\tfrac{1}{2}\sqrt{2x-3}+2\)
Verschuif de grijze grafiek met \(2\) naar boven.