Basisfuncties: Lineaire functies
 Eerstegraadsfuncties
Eerstegraadsfuncties
Afspraak is om \(f\) een eerstegraadsfunctie (een andere benaming voor lineaire functie) in \(x\) te noemen als het functievoorschrift geschreven kan worden als \[f(x)=a\,x+b,\]voor zekere getallen \(a\neq 0\) en \(b\).
De grafiek van \(f(x)=a\,x+b\) ontstaat uit de grafiek van de functie \(x\mapsto x\) door verticale vermenigvuldiging t.o.v. de \(x\)-as gevolgd door een verticale verschuiving.
De grafiek van \(f(x)=a\,x+b\) is een rechte lijn met richtingscoëfficiënt \(a\), ook wel hellingsgetal genoemd, en asafsnede \(b\).
Hieronder staat de grafiek van de lineaire functie \[T(t)=-\frac{2}{3}t+2\] waarin we met opzet eens andere variabelen dan de gangbare \(f\), \(x\) en \(y\) gebruiken. Je kunt hierbij denken aan een concentratie die in de loop van de tijd lineair afneemt (ook al moet je dan eigenlijk het domein zodanig inperken dat er geen negatieve waarden voor de grootheid ontstaan).
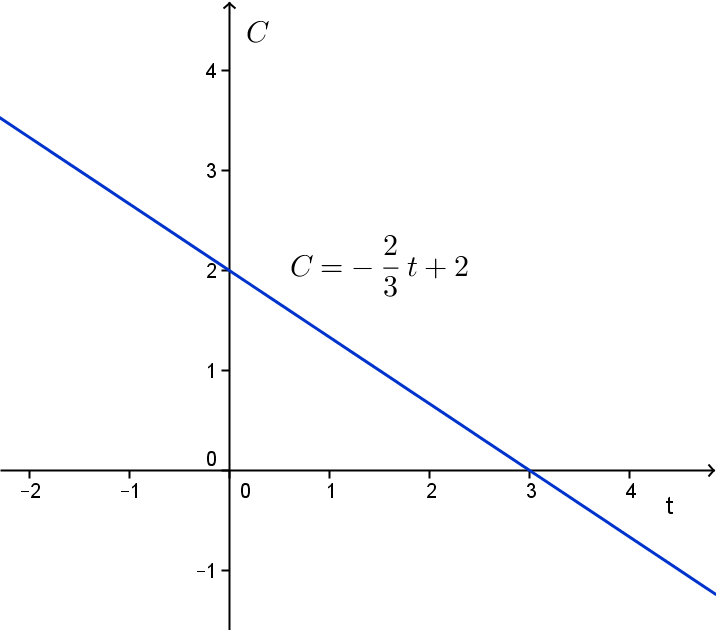
De richtingscoëfficiënt is terug te vinden in de grafiek. De richtingscoëfficiënt is namelijk het quotiënt van de toename \({\vartriangle}C\) van \(C=C(t)\) en de toename \({\vartriangle}t\) van \(t\). Bijvoorbeeld, tussen \(t=0\) en \(t=3\) neemt \(t\) toe met \({\vartriangle}t=3-0=3\), en \(C=C(t)\) met \({\vartriangle}C=0-2=-2\). Het quotiënt is dus \( \displaystyle \frac{{\vartriangle}C}{{\vartriangle}t }=\frac{-2}{3}=-\frac{2}{3}\).
De asafsnede is in dit geval rechtstreeks in de grafiek af te lezen omdat de functiewaarde voor \(t=0\) zichtbaar is. Als dit niet het geval is, dan moet je een ander punt, zeg \((C_1,t_1)\), in de grafiek aflezen en de asafsnede uitrekenen als \(C_1-a\cdot t_1\), onder de veronderstelling dat je de richtingscoëfficiënt \(a\) al eerder bepaald hebt.
Toepassing in beeldbewerking Een toepassing van lineaire functies in de beeldbewerking is lineaire helderheid- en contrastwijziging door de functie \[x\mapsto c\cdot x+b\] op de lichtintensiteit van elke pixel los te laten met positieve contrastparameter \(c\) (versterking als \(c>1\), afzwakking als \(0<c<1\)) en helderheidsparameter \(b\) (helderder als \(b>0\), donkerder als \(b<0\)).
Lineair model van een receptief veld van een neuron Het receptieve veld van een visuele zenuwcel is het gebied in het visuele veld, waarvan het vuurpatroon verandert wanneer het wordt gestimuleerd met bepaalde visuele prikkels. Stel dat de respons van een zenuwcel op het ene visuele beeld \(I_1\) een vuurpatroon is met frequentie \(r_1=20\;\text{Hz}\) en dat de respons op het andere visuele beeld \(I_2\) een vuurpatroon met frequentie \(r_2=40\;\text{Hz}\). In een lineair stimulus-responsmodel zal dan de respons van deze cel op bijvoorbeeld het gemiddelde \(\tfrac{1}{2}I_1+\tfrac{1}{2}I_2\) een vuurpatroon zijn met frequentie \(\tfrac{1}{2}r_1+\tfrac{1}{2}r_2=30\;\text{Hz}\). Als de ene stimulus, zeg \(I_2\) constant gehouden wordt en de andere stimulus \(I_1\) varieert, dan krijgen we in dit model een lineaire functie van de stimulus naar een vuurfrequentie.
Let op: dit is een wiskundig model met beperkingen want bij een sterke stimulus kan in dit model tot een onrealistisch hoge vuurfrequentie leiden.
Mathcentre video
Linear Functions (18:56)


