A second degree function of quadratic function in the variable \(x\) has function definition that can be written in standard form as \[f(x)=ax^2+bx+c\] where \(a\), \(b\) and \(c\) are numbers and \(a\neq 0\).

In the example on the right-hand side the function definition of one and the same quadratic function \(f(x)\) is written in various forms.

Examples

\[\begin{aligned}f(x) &= x^2+3x+2\\[0.25cm] f(x)&=(x+\tfrac{3}{2})^2-\tfrac{1}{4}\\[0.25cm]
f(x)&=(x+1)(x+2)\end{aligned}\]

The graph of such a function is called a parabola. It consists of points \((x,y)\) in the plane for which \(y=ax^2+bx+c\) is true.

If \(a>0\), then the graph is is an upward opening parabola, often called a a valley pa‍rabola.

If \(a<0\), then the graph is a downward opening parabola, often called a mountain pa‍rabola.

The graphs below illustrate this naming of parabola.

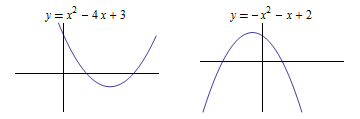
In the figure to the right other examples can be explored via the sliders.

A valley parabola has a point with a minimal value and a mountain parabola has a point with a maximal function value. The lowest or highest point of a parabola is called the vertex.
The \(x\)-coordinate of the vertex is equal to \(\displaystyle \frac{-b}{2a}\). The \(y\)-coordinate of the vertex is called an extreme value or, in short, an extremum. A quadratic function has a maximum value or a minimum value.

Every parabola has an axis of symmetry, namely the vertical line through the vertex splits the parabola into two parts that are mirror images of each other.

The parabola in the two examples above have two points in common with the horizontal axis. The \(x\)-coordinates of these points are called the zeros or roots of the quadratic function.

A parabola has 0, 1 or 2 zeros