Voorbeeld 1 Een voorbeeld van een kwadratisch verband is de wiskundige modellering van de gemiddelde lengtegroei van meisjes met het syndroom van Turner (een groeistoornis veroorzaakt door chromosomale afwijkingen waardoor meisjes o.a. vertraagde lengtegroei en geen puberteitsspurt doormaken). De gemiddelde lengte \(L(t)\) blijkt voor een leeftijd \(t\) groter dan drie jaar te modelleren via de volgende kwadratische functie: \[L(t) = -0.13t^2+6.3t+70.8,\] waarbij lengte \(L\) in cm en leeftijd \(t\) in jaren is uitgedrukt.

Voorbeeld 2 Het tweede voorbeeld is een wiskundig model voor een populatie met twee soorten; denk bijvoorbeeld aan een roofdier-prooidier systeem of in een microbiële context aan een populatie bestaande uit bacterieën en immuuncellen. Laat \(X_n\) en \(Y_n\) het aantal van soort X en Y in de populatie in jaar \(n\) zijn. Stel dat er geen interactie tussen de twee soorten is en de ontwikkeling van deze populatie beschreven kan worden door het volgende stelsel van differentievergelijkingen \[\begin{aligned} X_{n+1} &= a\cdot X_n+b\cdot Y_n\\ Y_{n+1} &= c\cdot X_n+d\cdot Y_n\end{aligned}\] voor zekere parameters \(a,\) \(b,\) \(c,\) \(d,\). Dan wordt het lange termijn verloop van de populatie bepaald door de oplossingen van de volgende kwadratische vergelijking in \(\lambda\): \[\lambda^2-(a+d)\cdot \lambda + (a\cdot d-b\cdot c) = 0\] Als voor alle oplossingen van deze vergelijking geldt dat ze in absolute waarde kleiner dan 1 zijn, dan sterft de populatie op termijn uit.

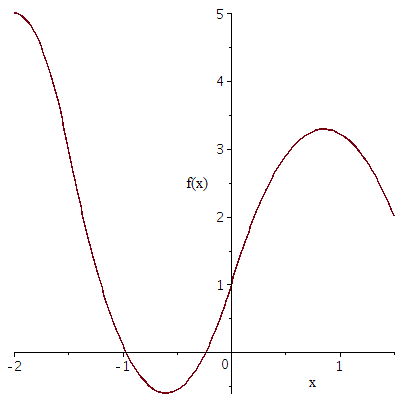
Voorbeeld 3. Het derde voorbeeld is een interpolatie van functiewaarden via zogenoemde kwadratische splines. Stel dat een functie \(f(x)\) is gedefinieerd op het interval \([-2,1.5]\) en dat alleen de volgende functiewaarden bekend zijn \[\begin{array}{c|c|c|c|c} x & -2 & -1.5 & 0 & 1.5 \\ \hline f(x) & 5 & 3 & 1 & 2\end{array}\] Je wilt nu toch functiewaarden kunnen uitrekenen op willekeurige punten in het interval \([-2, 1.5]\). Dit kun je doen door op de deelintervallen \([-2, -1.5]\), \([-1.5, 0]\) en \([0, 1.5]\) kwadratische functies \(f_1\), \(f_2\) en \(f_3\) te definiëren zodanig dat de functiewaarden in de randpunten overeenstemmen met de functiewaarden van \(f\) (bijvoorbeeld \(f_1(-1.5)=f_2(-1.5)=f(-1.5)\)) en een gladde grafiek ontstaat (d.w.z. de kwadratische functies zijn zo geconstructeerd dat de grafieken netjes in elkaar overvloeien zonder dat rare knikken in de randpunten zijn). Dergelijke functies \(f_1\), \(f_2\) en \(f_3\) op de drie deelintervallen heten kwadratische splines en ze kunnen gebruikt worden om functiewaarden uit te rekenen op de deelintervallen. In dit voorbeeld kun je nemen \[\begin{aligned} f_1(x) &= -8x^2-32x-27 \\ f_2(x) &= \tfrac{40}{9}x^2+\tfrac{16}{3}x +1\\ f_3(x) &= -\tfrac{28}{9}x^2+\tfrac{16}{3}x+1\end{aligned}\] Bij deze keuze start de grafiek van de benadering van \(f\) horizontaal in het punt \(x=-2\). Dit is een natuurlijke splines benadering van \(f\). Zie onderstaande grafiek van de natuurlijke splines benadering.