Three properties of polynomial functions

Basic functions: Polynomial functions

Three properties of polynomial functions

The function $f(x) = x^3 - 1$ is an example of a third degree function in $x$ with leading term $x^3$ . This polynomial can be written differently:

$x^3-1 = (x-1)(x^2+x+1)$ Check this by expanding brackets. The factor $x-1$ does not come completely out of the blue, but is a consequence of the fact that $x=1$ is a root of the polynomial, i.e., $f(1)=0$ . More generally, the following factor theorem holds:

If $f(x)$ a polynomial of degree $n\geq 1$ , and $a$ a real number for which $f(a)=0$ , then there is a polynomial $g(x)$ of grade $n-1$ such that $f(x)=(x-a)\cdot g(x)$ .

We do not discuss here the method of finding such a polynomial function $g(x)$ given a factor $x-a$ , except that we tell you that it works with the so-called long division of polynomials (similar to long division with numbers) and that in simple cases the polynomial function $g(x)$ can be computed by a direct method..

We consider the cubic polynomial $x^3-7x-6$ .
By looking carefully at the polynomial it can be noted that $x=-1$ is a root of the polynomial. This means that $x+1$ is a factor of the factorisation of the cubic polynomial and that

$x^3-7x-6=(x+1) (ax^2+bx+c)$ for some numbers $a$ , $b$ and $c$ . Removal of brackets in the right-hand side and collection of terms gives

$x^3-7x-6=ax^3+(a+b)x^2+(b+c)x+c$ Now we compare the coefficients of like terms on the left- and right-hand side annd find that

$a=1,\quad a+b=0,\quad b+c=-7,\quad c=-6$ In other words:

$a=1,\quad b=-1,\quad c=-6$ So:

$x^3-7x-6=(x+1)(x^2-x-6)$ By inspection we can factorise further:

$x^3-7x-6=(x+1)(x-3)(x+2)$ The roots of the cubic polynomial $x^3-7x-6$ are therefore $x=-1$ , $x=3$ and $x=-2$ .

$\phantom{x}$

A second important property of a polynomial function concerns factorisation with real coefficients. For this purpose we first note that a polynomial $p$ is irreducble if its degree is greater than 0 is and the polynomial cannot be written as a multiple of polynomials with lower nonzero degree, i.e., if the only divisors of $p$ are constants and constant multiples of $p$ .

Factorisation of polynomials with real coefficients Every polynomial can be factorized using only real numbers as coefficients as a product of linear and irreducible quadratic polynomials. This factorisation is unique up to a scalar and the ordering of the factors.

The factorisation of the polynomial $x^6+x^4-x^2-1$ is up to ordering of factors equal to $(x-1)(x+1)(x^2+1)^2$ .

$\phantom{x}$

A third important property of a polynomial function concerns asymptotic behaviour:

Asymptotics Consider the polynomial

$f(x)=a_nx^n+a_{n-1}x^{n-1} + \cdots + a_2x^2+a_1x+a_0$ with $a_n\neq 0$ . For large values of $x$ , the function value $f(x)$ is almost completely determined by the value of the leading term $a_nx^n$ .

In the above example of $f(x)=x^3-1$ is $f(1000)=(1000)^3-1=999999999\approx 1\,000\,000\,000=1000^3$ .

More generally: For large $x$ , the sign of $f(x)=a_nx^n+a_{n-1}x^{n-1} + \cdots + a_2x^2+a_1x+a_0$ is equal to the sign of the leading term $a_nx^n$ and depends on

the sign of $x$ (positive or negative),
the sign of $a_n$ , and
oddness or evenness of $n$ (After all, if $x$ is a negative number, then $x^n$ is negative if $n$ is odd and positive for even $n$ ).

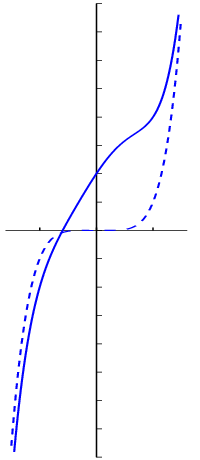
In the figure below, the graph of the fifth degree polynomial function

$f(x)=x^5-x^3-x^2+3x+2$ and the graph (dotted line) of the power function

$g(x)=x^5$ are plotted over the interval $(-1.6,1.6)$ . For the sake of clarity the horizontal axis is scaled differently than the vertical axis.
What you see is that the two graphs already come too close together when $|x|\approx 1.6$ . In general, $f(x)\approx g(x)$ for large $x$ . In other words,

$x^5-x^3-x^2+3x+2\approx x^5, \mathrm{\;for\;large\;values\;of\;}x.$

graph of polynomial function and an estimation

Mathcentre videos

Solving Cubic Equations (21:31)

$\phantom{x}$

Polynomial Division (13:57)