Basisfuncties: Veeltermfuncties
 Drie eigenschappen van veeltermfuncties
Drie eigenschappen van veeltermfuncties
De functie \(f(x) = x^3 - 1\) is een voorbeeld van een derdegraadsfunctie in \(x\) met kopterm \(x^3\). Deze veelterm kan ook anders opgeschreven worden: \[x^3-1 = (x-1)(x^2+x+1)\] Controleer dit door de haakjes weg te werken. De factor \(x-1\) komt overigens niet helemaal uit de lucht vallen, maar is een consequentie van het feit dat \(x=1\) een nulpunt van de veelterm is, d.w.z. \(f(1)=0\). Meer algemeen geldt de volgende factorstelling:
Factorstelling Als \(f(x)\) een veeltermfunctie van graad \(n\geq 1\) is en \(a\) een reëel getal waarvoor geldt dat \(f(a)=0\), dan is er een veelterm \(g(x)\) van graad \(n-1\) zodanig dat \(f(x)=(x-a)\cdot g(x)\).
Op de methode om zo'n veeltermfunctie \(g(x)\) te vinden gegeven een factor \(x-a\) gaan we niet verder in, behalve dat we verklappen dat het met staartdeling lukt (analoog aan staartdeling met getallen) en dat het in eenvoudige gevallen ook direct is uit te rekenen. Het volgende voorbeeld illustreert dit.
We bekijken de derdegraadsveelterm \(x^3-7x-6\).
Door goed kijken is in te zien dat \(x=-1\) een nulpunt van deze veelterm is. Dit betekent dat \(x+1\) een factor is in de factorontbinding van de de derdegraadsveelterm en dat \[x^3-7x-6=(x+1) (ax^2+bx+c)\] voor zeker getallen \(a\), \(b\) en \(c\). Wegwerken van de haakjes in het rechterlid en samennemen van termen geeft \[x^3-7x-6=ax^3+(a+b)x^2+(b+c)x+c\] We vergelijken nu de coëfficiënten links en rechts van gelijke machten en vinden dan dat \[a=1,\quad a+b=0,\quad b+c=-7,\quad c=-6\] oftewel \[a=1,\quad b=-1,\quad c=-6\] Dus: \[x^3-7x-6=(x+1)(x^2-x-6)\] Door inspectie kunnen we verder factoriseren tot \[x^3-7x-6=(x+1)(x-3)(x+2)\] De nulpunten van de derdegraadsveelterm \(x^3-7x-6\) zijn dus \(x=-1\), \(x=3\) en \(x=-2\).
\(\phantom{x}\)
Een tweede belangrijke eigenschap van veeltermfuncties betreft de ontbinding in factoren met reële coëffiënten. Hiervoor merken we eerst op dat een veelterm \(p\) onvereenvoudigbaar is als de graad van \(p\) groter dan 0 is en \(p\) niet geschreven kan worden als een veelvoud van een veelterm van kleinere graad groter dan 0, d.w.z. als de enige delers van \(p\) zijn constanten en constante veelvouden van \(p\).
Factorontbinding met reële coëfficiënten Elke veelterm is bij gebruik van de verzameling van reële getallen op een scalair en volgorde van factoren na uniek te ontbinden in lineaire factoren en onvereenvoudigbare kwadratische factoren.
De factorontbinding van \(x^6+x^4-x^2-1\) is gelijk aan \((x-1)(x+1)(x^2+1)^2\).
\(\phantom{x}\)
Een derde belangrijke eigenschap van veeltermfuncties betreft asymptotisch gedrag:
Asymptotiek Bekijk de veeltermfunctie \[f(x)=a_nx^n+a_{n-1}x^{n-1} + \cdots + a_2x^2+a_1x+a_0\] met \(a_n\neq 0\). Voor grote waarden van \(x\) wordt de functiewaarde \(f(x)\) bijna helemaal bepaald door de waarde van de kopterm \(a_nx^n\).
In bovenstaand voorbeeld van \(f(x)=x^3-1\) is \(f(1000)=(1000)^3-1=999999999\approx 1\,000\,000\,000=1000^3\).
Meer algemeen, voor grote waarden van \(x\) is het teken van \(f(x)=a_nx^n+a_{n-1}x^{n-1} + \cdots + a_2x^2+a_1x+a_0\) gelijk aan het teken van de kopterm \(a_nx^n\) en hangt deze af van
- het teken van \(x\) (positief of negatief),
- het teken van \(a_n\), en
- het even or oneven zijn van \(n\) (Immers als \(x\) een negatief getal is, dan is \(x^n\) negatief als \(n\) oneven is en positief voor even \(n\)).
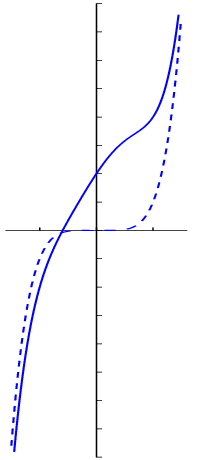
In onderstaande figuur is de grafiek van de vijfdegraadsveeltermfunctie \[f(x)=x^5-x^3-x^2+3x+2\] getekend, samen met de grafiek (in stippellijn) van de machtsfunctie \[g(x)=x^5\] over het interval \((-1.6,1.6)\). Voor de duidelijkheid is de horizontale as anders geschaald dan de verticale as.
Wat je ziet is dat de beide grafieken al dicht bij elkaar komen te liggen als \(|x|\approx 1.6\). In het algemeen geldt \(f(x)\approx g(x)\) voor grote \(x\). Met andere woorden: \[x^5-x^3-x^2+3x+2\approx x^5, \mathrm{\;voor\;grote\;}x.\]
Mathcentre videos
Solving Cubic Equations (21:31)
#\phantom{x}#
Polynomial Division (13:57)


