Basic functions: Rational functions
Definition and basic properties
Fractional linear function
The power function \(\displaystyle f(x)=x^{-1}=\frac{1}{x}\) is an example of a fractional linear function. The function is called fractional because it contains a 'fraction' with linear expressions in both the numerator and the denominator. Its graph is called a hyperbola and is split into two pieces separated by a vertical asymptote and horizontal asymptote. These are the dotted lines in the figure on the right-hand side.
When the value of \(x\) is close to \(0\), then the point \((x,f(x))\) is near the vertical line \(x=0\), the vertical asymptote. In \(x=0\), \(f(x)\) is not defined.
When the absolute value of \(x\) gets larger and larger, then the point \((x,f(x))\) comes ever closer to the horizontal line \(y=0\), the horizontal asymptote. In other words, this means \(f(x)\to 0\) as \(x\to \pm\infty\).
Asymptote An asymptote is a line where the graph of a function gets closer and closer, and where the graph eventually appears to coincide.
Let's look at a simple variant: \[f(x) = \frac{10}{x-3}+2\]
The graph of \(f(x) = \frac{10}{x-3}+2\) is similar to that of \(\displaystyle\frac{1}{x}\): it is the obtained from the graph of \(x\mapsto\frac{1}{x}\) by a horizontal translation over a distance \(3\) to the right, followed by a vertical multiplication by \(10\), and a vertical translation by \(2\). The main difference is that the vertical and horizontal asymptotes are given by the equations \(x=3\) and \(y=2\), respectively. This means that\(f(x)\to 2\) as \(x\to \infty\) and \(f(x)\to 2\) as \(x\to -\infty\).
Also, the function is in \(x=3\) not defined, but we do know that the function value \(f(x)\) becomes, in absolute sense, very large when \(x\) approaches \(x=3\). More precisely, \(f(x)\to\infty\) as \(x\downarrow 3\) and \(f(x)\to-\infty\) as \(x\uparrow 3\), where the arrows \(\downarrow\) and \(\uparrow\) mean that a domain value is approached from the right- and left-hand side, respectively.
One can also write the above function rule in a different way: \[\begin{aligned}\frac{10}{x-3}+2&= \frac{10}{x-3}+\frac{2(x-3)}{x-3}\\[0.25cm] &=\frac{10+2(x-3)}{x-3}\\[0.25cm] &=\frac{2x+4}{x-3}\end{aligned}\] So the function rule is a quotient of two linear expressions. We speak of a fractional linear function .
Fractional linear function
A fractional linear function is a function that can be written in the form \[f(x)=\frac{ax+b}{cx+d}\] with numbers \(a,b,c,d\) with \(c\neq 0\) and \(ad\neq bc\). The graph of such a function is called a hyperbola. The requirement \(ad\neq bc\) prevents the function from reducing to a linear or constant function. Hyperbolas have a vertical and horizontal asymptote; with the chosen standard form, these are the lines \(x=-\frac{d}{c}\) and \(y=\frac{a}{c}\), respectively.
By moving the sliders in the adjacent figure you get an idea of what the graph of the fractional linear function \[f(x)=\dfrac{ax+b}{cx+d}\] looks like.
A fractional linear function is a special case of a rational function.
Rational function In general, any function whose function can be reduced to a quotient of polynomials is called a rational function. Such a function is of the form \[f(x)=\frac{a(x)}{b(x)}=\frac{a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x+b_0}\]
Calculation rules The calculation rules for rational functions are the usual rules for manipulating mathematical formulas, with the understanding that the domain on which the functions are defined can differ
(see Precalculus: Fractions with letters, Simplifying fractions ).
If \(a\), \(b\), \(c\) and \(d\) are polynomials, then the following calculation rules apply to the domains in which the left- and right-hand sides are both defined:
- \(\displaystyle\quad \dfrac{a}{b}+\dfrac{c}{d} = \dfrac{ad+bc}{bd}\)
- \(\displaystyle\quad \dfrac{a}{b}+\dfrac{c}{b} = \dfrac{a+c}{b}\)
- \(\displaystyle\quad \dfrac{c\cdot a}{c\cdot b} = \dfrac{a}{b}\)
- \(\displaystyle\quad c\cdot \dfrac{a}{b} = \dfrac{c\cdot a}{b}\)
- \(\displaystyle\quad \dfrac{a}{b}\cdot\frac{c}{d} = \dfrac{a\cdot c}{b\cdot d}\)
- \(\displaystyle\quad \frac{\dfrac{a}{b}}{ \dfrac{c}{d}}= \dfrac{a\cdot d}{b\cdot c}\)
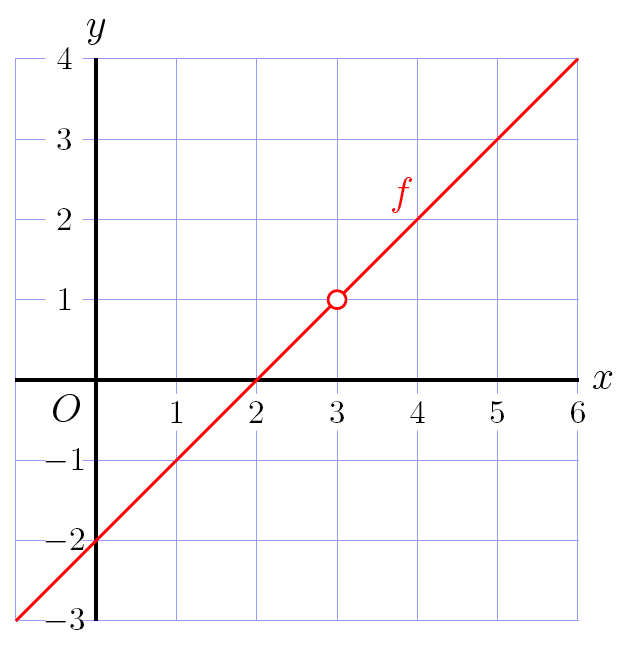
Perforation The third rule means for example that \[\dfrac{x^2-5x+6}{x-3}=\dfrac{(x-2)(x-3)}{x-3}=x-2\] But there is a small difference: where the left-hand side is not defined in \(x=3\), the right-hand side as a linear function is well-defined with function value \(1\). When you draw the graphs of the left- and right-hand sides on their domain, you will not see any difference either: the function value for the rational function gets close to \(1\) when the original is near \(3\). We call \(x=3\), a point where the rational expression is not defined, a perforation.
Visualisation
The graph of \(f(x)=\dfrac{x^2-5x+6}{x-3}\) appears to be a straight line, but the open circle indicates that the function is not defined for \(x=3\). We call this point a perforation, a point where the function value does not exist, but the limit does exist. In this case, \(f(3)\) does not exist, because both the numerator and denominator are zero in \(x=3\). A hole has been created in the graph of \(f\), causing the graph to break at \(x=3\).
Asymptotics in rational functions Assuming that there are no common factors in the two polynomials \(a(x)\) and \(b(x)\), the vertical asymptotes of the rational function \(\frac{a(x)}{b(x)}\) are described by the equations \(x=\alpha\) with \(b(\alpha)=0\). In other words, the vertical asymptotes of a rational function are found at the zeros of the polynomial in the denominator of the function rule.
The behaviour for large values of the independent variable depends on the degrees of the polynomials in numerator and denominator because \(\displaystyle f(x)\approx \frac{a_nx^n}{b_mx^m}=\frac{a_n}{b_n}x^{n-m}\) as \(x\to\pm \infty\).
It follows, for example, that once \(m>n\), then \(f(x)\to 0\) as \(x\to\pm\infty\).
Mathcentre video
Simplification of Algebraic Fractions (17:33)
