Basisfuncties: Rationale functies
Definitie en basiseigenschappen
Gebroken functie
De machtsfunctie \(\displaystyle f(x)=x^{-1}=\frac{1}{x}\) is een voorbeeld van een gebroken functie. De functie heet gebroken omdat de grafiek, een hyperbool genaamd, opgesplitst is in twee stukken gescheiden door een verticale asymptoot en horizontale asymptoot. Dit zijn in de figuur rechts de gestippelde lijnen.
Als de \(x\)-waarde in de buurt komt van \(0\), dan komt het bijpassende punt \((x,f(x))\) dicht bij de verticale lijn \(x=0\), de verticale asymptoot. In \(x=0\) is \(f(x)\) niet gedefinieerd.
Als de absolute waarde van \(x\) zeer groot is, dan komt het bijpassende punt \((x,f(x))\) dicht bij de horizontale lijn \(y=0\), de horizontale asymptoot. Anders opgeschreven betekent dit dat \(f(x)\to 0\) als \(x\to \pm\infty\).
Asymptoot Een asymptoot is een lijn waar de grafiek van een functie steeds dichterbij in de buurt komt te liggen en waar de grafiek uiteindelijk mee samen lijkt te vallen.
Laten we eens naar een eenvoudige variant kijken: \[f(x) = \frac{10}{x-3}+2\]
De grafiek van \(f(x) = \frac{10}{x-3}+2\) lijkt op die van \(\displaystyle\frac{1}{x}\): de grafiek wordt verkregen door horizontale translatie naar rechts over een afstand \(3\), gevolgd door een verticale vermenigvuldiging met \(10\) en een verticale translatie met \(2\). Het belangrijkste verschil is dat de verticale respectievelijk horizontale asymptoot gegeven zijn door de vergelijkingen \(x=3\) en \(y=2\). Dit betekent dat \(f(x)\to 2\) als \(x\to \infty\) en \(f(x)\to 2\) als \(x\to -\infty\).
Ook is de functie in \(x=3\) niet gedefinieerd, maar weten we wel dat de functiewaarde \(f(x)\) zeer groot wordt als \(x\) in de buurt van \(x=3\) komt. Meer precies, \(f(x)\to\infty\) als \(x\downarrow 3\) en \(f(x)\to-\infty\) als \(x\uparrow 3\), waarbij de pijlen \(\downarrow\) en \(\uparrow\) betekenen dat je een domeinwaarde nadert vanuit de rechter- respectievelijk linkerkant.
Je kunt bovenstaande functie ook anders opschrijven: \[\begin{aligned}\frac{10}{x-3}+2&= \frac{10}{x-3}+\frac{2(x-3)}{x-3}\\[0.25cm] &=\frac{10+2(x-3)}{x-3}\\[0.25cm] &=\frac{2x+4}{x-3}\end{aligned}\] Het functievoorschrift is dus een quotiënt van twee lineaire uitdrukkingen. We spreken van een gebroken lineaire functie.
Gebroken lineaire functie
Een gebroken lineaire functie is een functie van de vorm \[f(x)=\frac{ax+b}{cx+d}\] met \(a,b,c,d\) getallen met \(c\neq 0\) en \(ad\neq bc\) en de grafiek van een dergelijke functie heet een hyperbool. De eis \(ad\neq bc\) voorkomt dat de functie reduceert tot een lineaire of constante functie. Hyperbolen hebben een verticale en horizontale asymptoot; bij de gekozen standaardvorm zijn dat de lijnen \(x=-\frac{d}{c}\) resp. \(y=\frac{a}{c}\).
Door de sliders in nevenstaande figuur te bewegen krijg je een idee hoe de grafiek van de gebroken lineaire functie \[f(x)=\dfrac{ax+b}{cx+d}\] er uit ziet.
Een gebroken lineaire functie is een speciaal geval van een rationale functie.
Rationale functie
Men noemt in het algemeen elke functie waarvan het functievoorschrift herleid kan worden tot een quotiënt van veeltermen een rationale functie. Zo'n functie is van de vorm \[f(x)=\frac{a(x)}{b(x)}=\frac{a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x+b_0}\]
Voorbeeld
\[f(x)=\frac{x}{x^2+1}\]
Rekenregels De rekenregels voor rationale functies zijn de gebruikelijke regels voor het manipuleren van wiskundige formules, met dien verstande dat het domein waarop de functies gedefinieerd zijn kan afwijken
(zie Precalculus: Breuken met letters, Breuken vereenvoudigen).
Als \(a\), \(b\), \(c\) en \(d\) veeltermen zijn, dan gelden de volgende rekenregels op de domeinen waarin linker- en rechterlid beide gedefinieerd zijn:
- \(\displaystyle\quad \dfrac{a}{b}+\dfrac{c}{d} = \dfrac{ad+bc}{bd}\)
- \(\displaystyle\quad \dfrac{a}{b}+\dfrac{c}{b} = \dfrac{a+c}{b}\)
- \(\displaystyle\quad \dfrac{c\cdot a}{c\cdot b} = \dfrac{a}{b}\)
- \(\displaystyle\quad c\cdot \dfrac{a}{b} = \dfrac{c\cdot a}{b}\)
- \(\displaystyle\quad \dfrac{a}{b}\cdot\frac{c}{d} = \dfrac{a\cdot c}{b\cdot d}\)
- \(\displaystyle\quad \frac{\dfrac{a}{b}}{ \dfrac{c}{d}}= \dfrac{a\cdot d}{b\cdot c}\)
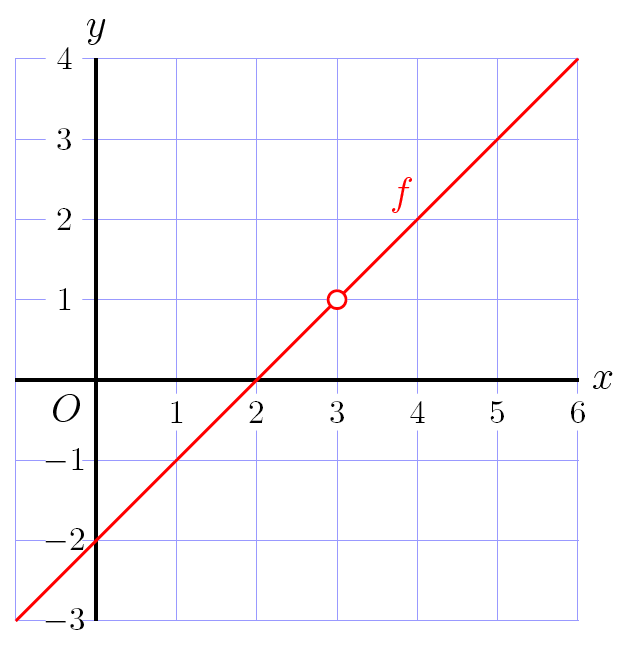
Perforatie De derde rekenregel betekent bijvoorbeeld dat \[\dfrac{x^2-5x+6}{x-3}=\dfrac{(x-2)(x-3)}{x-3}=x-2\] Maar er is een klein verschil: waar het linkerlid niet gedefinieerd is in \(x=3\), is het rechterlid als lineaire functie gewoon wel goed gedefinieerd met functiewaarde \(1\). Als je de grafieken van linker- en rechterlid op hun domein tekent zul je ook geen verschil zien: de functiewaarden voor de rationale functie komen dicht bij \(1\) te liggen als het origineel dicht bij \(3\) ligt. We noemen \(x=3\), een punt waar de rationale uitdrukking niet gedefinieerd is, een perforatie .
Visualisatie
De grafiek van \(f(x)=\dfrac{x^2-5x+6}{x-3}\) lijkt een rechte lijn, maar het open rondje geeft aan dat de functie niet gedefinieerd is voor \(x=3\). Dit punt noemen we een perforatie, een punt waar de functiewaarde niet bestaat, maar de limiet wel. In dit geval bestaat \(f(3)\) niet, omdat zowel de teller als de noemer de waarde \(0\) hebben in \(x=3\). Er is een punt uit de grafiek gehaald, waardoor de grafiek wordt onderbroken bij \(x=3\).
Asymptotiek bij rationale functies
Onder de veronderstelling dat er geen gemeenschappelijke factoren in de twee veeltermen \(a(x)\) en \(b(x)\) voorkomen worden de verticale asymptoten van de rationale functie \(\frac{a(x)}{b(x)}\) beschreven door de vergelijkingen \(x=\alpha\) met \(b(\alpha)=0\). Met andere woorden, de verticale asymptoten van een rationale functie horen bij de nulpunten van de veelterm in de noemer van het functievoorschrift.
Het gedrag voor grote waarden van de onafhankelijke variabele hangt af van de graden van de veeltermen in teller en noemer want \(\displaystyle f(x)\approx \frac{a_nx^n}{b_mx^m}=\frac{a_n}{b_n}x^{n-m}\) als \(x\to\pm \infty\).
Hieruit volgt bijvoorbeeld dat zodra \(m>n\), dan \(f(x)\to 0\) als \(x\to\pm\infty\).
Voorbeeld
\[f(x)=\frac{1}{x^2-1}\]
Mathcentre video
Simplification of Algebraic Fractions (17:33)
