Basic functions: Power functions
Power functions with positive fractional exponents
The best known power function with a fractional exponent is the square root \(x\mapsto \sqrt{x}\); this can also be written in power notation because \[\sqrt{x}=x^{\frac{1}{2}}\] For a higher power root we can also convert the root notation into power notation so that it is clear that it is actually a power function: \[\sqrt[n]{x}=x^{\frac{1}{n}}\quad\text{for }n=3,4,5,\ldots\] Through the calculation rules we can also define power functions that have a positive fraction as exponent: for an irreducible fraction \(\tfrac{t}{n}\) we agree on the following: \[x^{\frac{t}{n}}=\left(x^{\frac{1}{n}}\right)^t=\left(\sqrt[n]{x}\right)^t\] One can of course also choose \[x^{\frac{t}{n}}=\left(x^{t}\right)^{\frac{1}{n}}=\sqrt[n]{x^{t}}\] because it does not matter for the result.
Some examples of power function with a fraction as exponent and some rewritings in square root notation: \[\begin{aligned}x^{\frac{2}{3}}&=\sqrt[3]{x^2}\\[0.25cm] x^{\frac{3}{2}}&=\sqrt{x^3}\\ &=x\sqrt{x}\\[0.25cm] x^{\frac{5}{3}}&=\sqrt[3]{x^5}\\ &=x\sqrt[3]{x^2}\\ &=\frac{x^2}{\sqrt[3]{x}}\end{aligned}\]
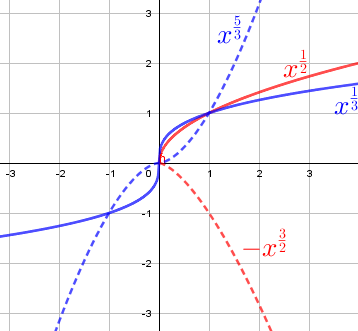
Below are the graphs of various power functions with fractions as exponents. The function rules are listed with the graphs.
