Basisfuncties: Machtsfuncties
 Machtsfuncties met positieve gebroken exponenten
Machtsfuncties met positieve gebroken exponenten
De bekendste machtsfunctie met een gebroken exponent is de vierkantwortelfunctie \(x\mapsto \sqrt{x}\); deze is namelijk ook te schijven in machtsnotatie omdat \[\sqrt{x}=x^{\frac{1}{2}}\] Ook voor een hogere-machtswortel kunnen we de wortelnotatie omzetten in machtsnotatie zodat duidelijk is dat het eigenlijk om een machtsfunctie gaat: \[\sqrt[n]{x}=x^{\frac{1}{n}}\quad\text{voor }n=3,4,5,\ldots\] Via de rekenregels kunnen we dan ook machtsfuncties definiëren die een positieve breuk als exponent hebben: voor een onvereenvoudigbare breuk \(\tfrac{t}{n}\) spreken we het volgende af: \[x^{\frac{t}{n}}=\left(x^{\frac{1}{n}}\right)^t=\left(\sqrt[n]{x}\right)^t\] Er kan natuurlijk ook gekozen worden voor \[x^{\frac{t}{n}}=\left(x^{t}\right)^{\frac{1}{n}}=\sqrt[n]{x^{t}}\] want voor het resultaat maakt niet uit.
Enkele voorbeelden van machtsfunctie met een breuk als exponent en enkele herschrijvingen in wortelnotatie: \[\begin{aligned}x^{\frac{2}{3}}&=\sqrt[3]{x^2}\\[0.25cm] x^{\frac{3}{2}}&=\sqrt{x^3}\\ &=x\sqrt{x}\\[0.25cm] x^{\frac{5}{3}}&=\sqrt[3]{x^5}\\ &=x\sqrt[3]{x^2}\\ &=\frac{x^2}{\sqrt[3]{x}}\end{aligned}\]
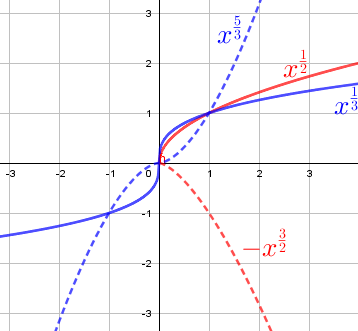
Hieronder staan de grafieken van verschillende machtsfuncties met breuken als exponenten. Het functievoorschrift staat bij de grafieken vermeld.