Basic functions: Rational functions
An oblique asymptote of a rational function
Some rational functions have an oblique asymptote (or slant asymptote) instead of a horizontal asymptote. This is the case for rational functions where the degree of the numerator is one higher than the degree of the denominator. The example below illustrates this.
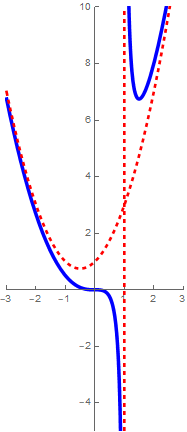
Consider the rational function \[f(x)=\frac{2x^2-x}{x-1}\] The graph of \(f\) is shown in the diagram, on the right-hand side, together with the vertical asymptote and a slanted line that the graph of \(f\) for large absolute values of \(x\).
Long division leads to \[\frac{2x^2-x}{x-1}=2x+1+\frac{1}{x-1}\] For large values of \(x\), the term \(\frac{1}{x-1}\) is small and the function value \(f(x)\) is close to that of the function \(x\mapsto 2x+1\). Graphically this means that the graph of \(f\) for large values of\(x\) approaches the graph of the line \(y=2x+1\). The same happens with increasingly negative values of \(x\). In formula language: \[\lim_{x\to\pm\infty}\bigl(f(x)-(2x+1)\bigr)=0\]
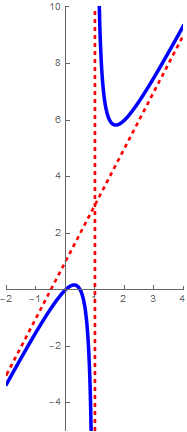
Suppose that \(f(x)=\frac{p(x)}{q(x)}\) is a rational function with \(\mathrm{degree}(p) = \mathrm{degree}(q)+1\). The line with the equation \(y=a\,x+b\), for certain numbers \(a\) and \(b\), is an oblique asymptote or slant asymptote of (the graph of) \(f\) if and only if \[\lim_{x\to\infty}\bigl(f(x)-(a\,x+b)\bigr)=0\quad\text{or}\quad\lim_{x\to-\infty}\bigl(f(x)-(a\,x+b)\bigr)=0\]
Asymptotics of a rational function \(f(x)=\frac{p(x)}{q(x)}\) with \(\mathrm{graad}(p) > \mathrm{degree}(q)+1\) is also possible, but then the function approaches for large values of \(x\) the polynomial function defined as the quotient of long division of the numerator by the denominator. For example, for the function \[f(x)=\frac{x^3}{x-1}\] long division leads to \[f(x)=x^2+x+1 + \frac{1}{x-1}\] and thus the graph of \(f\) approaches the parabola \(y=x^2+x+1\). See the diagram on the right-hand side.
