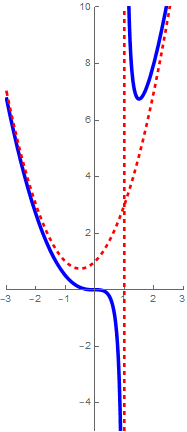
Basisfuncties: Rationale functies
Scheve asymptoot van een rationale functie
Sommige rationale functies hebben een scheve asymptoot in plaats van een horizontale asymptoot. Dit is het geval bij rationale functies waarvan de graad van de teller één hoger is dan de graad van de noemer. Onderstaand voorbeeld illustreert dit.
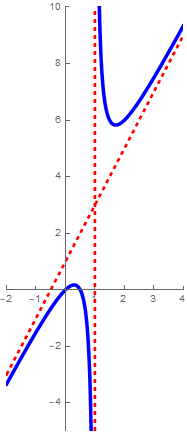
Bekijk de rationale functie \[f(x)=\frac{2x^2-x}{x-1}\] De grafiek van \(f\) is in nevenstaand diagram getekend, samen met de verticale asymptoot en een schuine lijn waartoe de grafiek van \(f\) voor grote absolute waarden van \(x\) nadert.
Als we delen met rest toepassen krijgen we \[\frac{2x^2-x}{x-1}=2x+1+\frac{1}{x-1}\] Voor grote waarden van \(x\) wordt de term \(\frac{1}{x-1}\) klein en ligt de functiewaarde \(f(x)\) dicht bij die van de functie \(x\mapsto 2x+1\). Grafisch betekent dit dat de grafiek van \(f\) voor grote waarden \(x\) van steeds meer nadert tot de grafiek van de lijn \(y=2x+1\). Hetzelfde gebeurt bij steeds negatievere waarden van \(x\). In formuletaal: \[\lim_{x\to\pm\infty}\bigl(f(x)-(2x+1)\bigr)=0\]
Stel dat \(f(x)=\frac{p(x)}{q(x)}\) een rationale functie is met \(\mathrm{graad}(p) = \mathrm{graad}(q)+1\). De rechte lijn met vergelijking \(y=a\,x+b\), voor zekere getallen \(a\) en \(b\), is een scheve asymptoot van (de grafiek van) \(f\) dan en slechts dan als \[\lim_{x\to\infty}\bigl(f(x)-(a\,x+b)\bigr)=0\quad\text{of}\quad\lim_{x\to-\infty}\bigl(f(x)-(a\,x+b)\bigr)=0\]
Asymptotiek van een rationale functie \(f(x)=\frac{p(x)}{q(x)}\) met \(\mathrm{graad}(p) > \mathrm{graad}(q)+1\) is ook mogelijk, maar dan nadert de functie voor grote waarden van \(x\) de veeltermfunctie die je krijgt als quotiënt bij deling met rest van de teller door de noemer. Bijvoorbeeld, voor de functie \[f(x)=\frac{x^3}{x-1}\] krijgen we bij deling met rest \[f(x)=x^2+x+1 + \frac{1}{x-1}\] en dus nadert de grafiek van \(f\) de parabool \(y=x^2+x+1\). Zie nevenstaand diagram.
