Exponential functions and logarithms: Exponential functions
 Definition and basic properties
Definition and basic properties
We have already seen that a power function in \(x\) consists of a power \(x^p\), for a certain number \(p\). The quadratic function with definition \(x^2\) is a simple example. An exponential function also consists of a power, but in this case, the independent variable \(x\) is the exponent, such as, for example, in the function definition \(2^x\).
A function of the form \(f(x)=a^x\) for \(a>0, a\neq 1\) is called an exponential function with base \(a\).
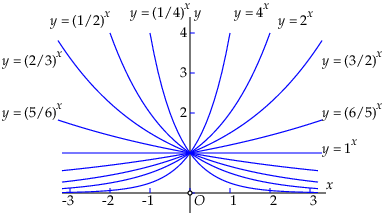
The diagram on the right-hand side shows the graph of \(a^x\) for some values of \(a\).
The domain of an exponential function is \(\mathbb{R}\) and its range is the open interval \((0,\infty)\).
Examples
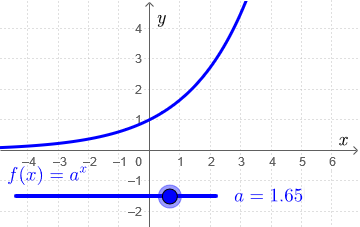
Interactive visualisation By moving the slider in the below interactive figure below you can get an idea how the graph of the exponential function \[f(x)=a^x\] looks like for various values of the base \(a\).
Properties Some properties of an exponential function \(f(x)=a^x\):
- \(f(0)=1\) (each graph of an exponential function goes through the point (0,1)).
- \(f(x)>0\) for all \(x\).
- \(f\) is increasing if and only if \(a>1\). The larger \(a\), the faster the function increases.
- \(f\) is decreasing if and only if \(0<a<1\). The closer \(a\) is to 0, the faster the function decreases.
- The horizontal axis is a horizontal asymptote for each exponential function.
If \(0<a<1\), then the function values \(a^x\) are small for large positive values of \(x\) (in mathematical language: \(a^x\to 0\) as \(x\to\infty\), or even more formal, \(\lim_{x\to \infty}a^x=0\) ). If \(a>1\) , then \(\lim_{x\to -\infty}a^x=0\)). - Exponential functions grow faster than polynomials. In mathematical terminology: voor the base \(a>1\) en natural number \(n\) there exists a number \(N\) such that \(a^x>x^n\) for all \(x>N\). You could choose \(N=2n+1+\frac{2^n(n+1)!}{(a-1)^{n+1}}\) .
Mathcentre video
Exponential Functions (18:18)