Exponentiële functies en logaritmen: Exponentiële functies
 Definitie en basiseigenschappen
Definitie en basiseigenschappen
Een machtsfunctie in \(x\) bestaat uit een macht \(x^p\), voor zeker getal \(p\). De kwadraatfunctie met functievoorschrift \(x^2\) is een eenvoudig voorbeeld. Een exponentiële functie bestaat ook uit een macht, maar in dit geval staat de onafhankelijke variabele \(x\) in de exponent, bijvoorbeeld zoals in het functievoorschrift \(2^x\).
Een functie van de vorm \(f(x)=a^x\) voor \(a>0, a\neq 1\) heet een exponentiële functie met grondtal \(a\).
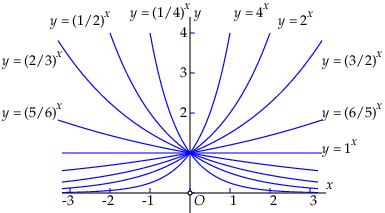
In nevenstaande figuur is voor enige waarden van \(a\) de grafiek van \(a^x\) getekend.
Het domein van een exponentiële functie is \(\mathbb{R}\) en het bereik is het open interval \((0,\infty)\).
Voorbeelden
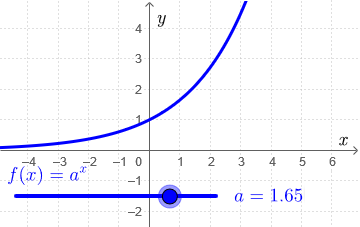
Interactieve visualisatie Door de schuifbalk in onderstaande interactieve visualisatie te verslepen krijg je een idee hoe de grafiek van de exponentiële functie \[f(x)=a^x\] er uit ziet voor verschillende waarden van het grondtal \(a\).
Eigenschappen Enkele eigenschappen van een exponentiële functie \(f(x)=a^x\):
- \(f(0)=1\) (elke grafiek van een exponentiële functie gaat door het punt (0,1)).
- \(f(x)>0\) voor alle \(x\).
- \(f\) is stijgend dan en slechts dan als \(a>1\). Hoe groter \(a\), hoe sneller de functie stijgt.
- \(f\) is dalend dan en slechts dan als \(0<a<1\). Hoe dichter \(a\) bij 0 ligt, hoe sneller de functie daalt.
- De horizontale as treedt voor elke exponentiële functie op als horizontale asymptoot.
Als \(0<a<1\), dan zijn functiewaarden \(a^x\) voor grote positieve \(x\) klein (in wiskundetaal: \(a^x\to 0\) als \(x\to\infty\), of nog formeler \(\lim_{x\to \infty}a^x=0\)). Als \(a>1\), dan \(\lim_{x\to -\infty}a^x=0\)). - Exponentiële functies 'groeien harder' dan veeltermen. In wiskundige terminologie: voor een grondtal \(a>1\) en natuurlijk getal \(n\) geldt dat er een getal \(N\) bestaat zodanig dat \(a^x>x^n\) voor alle \(x>N\). Je zou \(N=2n+1+\frac{2^n(n+1)!}{(a-1)^{n+1}}\) kunnen kiezen.
Mathcentre video
Exponential Functions (18:18)